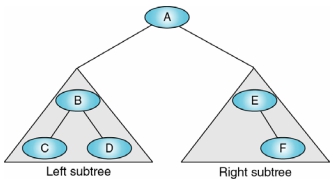
使用 Limit 來決定 Order
Limit

- 邏必達法則 (L’ Hospital Rule)
通常在針對某一問題開發程式時,都會經過下列步驟:
定義問題演算法,並評估其執行效率程式,並加以測試
Vertices )Edges or arcs )m-way Search Tree 雖利用增大 Tree 的 Degree 來降低 Search Tree 的高度,以減少 Disk I/O 的次數,但若此 Tree 不平衡,也可能會變相地增加 Disk I/O 的次數
B-tree of order m是一個 Balanced m-way search tree。可以為空,若不為空,則滿足:
Root: 2 ≤ degree ≤ m)⎡m/2⎤ ≤ degree ≤ m)m-way Search Tree 主要用於外部搜尋 (External Search)
Memory 中進行 search 之工作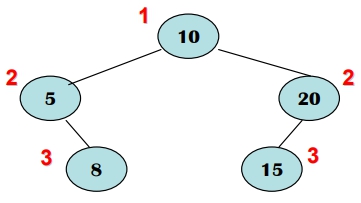
平衡的 Binary Search Tree,其平均比較次數愈小,Big-O ≈ O (log n)偏斜的 Binary Search Tree,其平均比較次數愈大,Big-O ≈ O (n)靜態的環境下,一般 Binary Search Tree 的建構方法可以有較充裕的時間將欲搜尋的所有資料建構成較平衡的 Binary Search Tree,以提升後續資料搜尋時的效率動態的環境下,資料可以隨時 Insert / Delete。此時,一般 Binary Search Tree 的建構方法會産生 Skewed Binary Tree,導致資料搜尋的效率變差 (即:O (n))AVL Tree 讓 Tree 的高度均維持在高度平衡的情況
具有 External Node 的 B.T. 稱之
n+1 條空 Link,在這些空 Link 上加上特定節點,稱為 External Node (或 Failure Node),其餘 Nodes 稱 Internal Nodes二元搜尋樹的角度來説,若搜尋到外部節點時,代表在原本的二元樹中找不到想要的資料,也就是搜尋失敗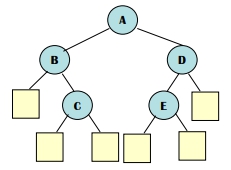
Depth First Search (DFS;深先搜尋,需利用 Stack)Breadth First Search (BFS;廣先搜尋,需利用 Queue)≥ 0 個 nodes 所構成的有限集合