Graph Traversal

發表於 Disqus：
文章字數： 2.3k 所需閱讀時間 ≈ 4 分鐘
  • 目的：
    • 圖形中的所有頂點都被拜訪到，且僅被拜訪到一次
  • 拜訪方式有兩種：
    • Depth First Search (DFS；深先搜尋，需利用 Stack)
    • Breadth First Search (BFS；廣先搜尋，需利用 Queue)
  • 應用：
    • 檢査 Graph 是否連通？
    • 找出此圖的連通單元
    • ...
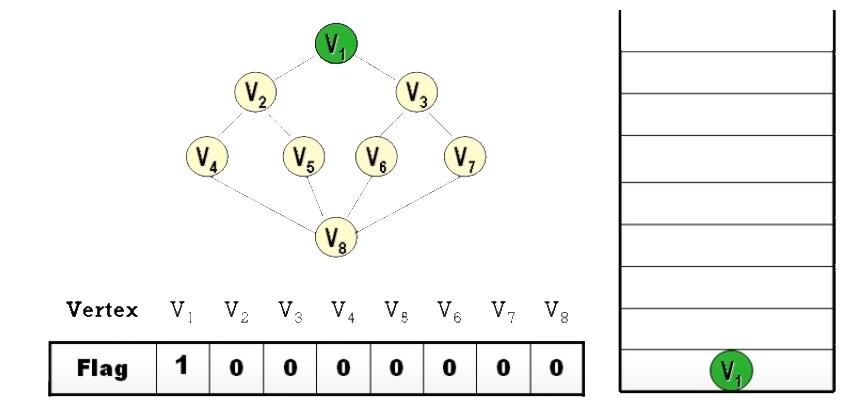
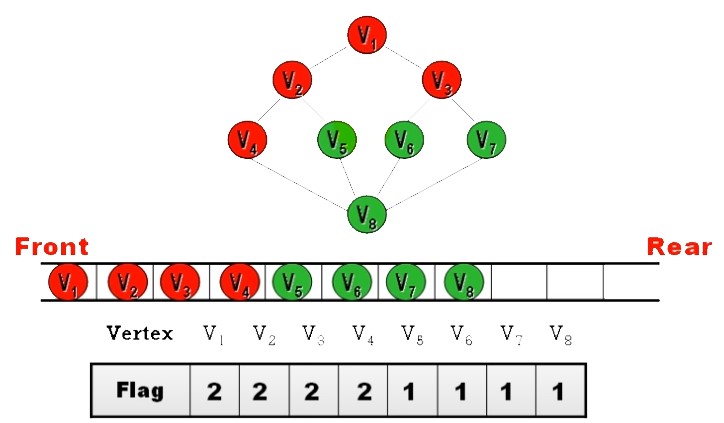
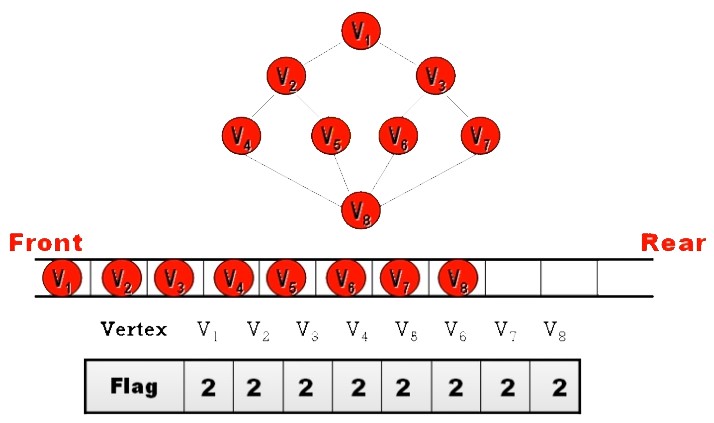
  • 不論是採用何種圖形追蹤方法，在實作上皆可引入一個 visited flag (拜訪旗標)，以指出頂點的目前状況
    • Flag = 0：尚未拜訪 (not processed)
    • Flag = 1：拜訪中 (in queue or stack)
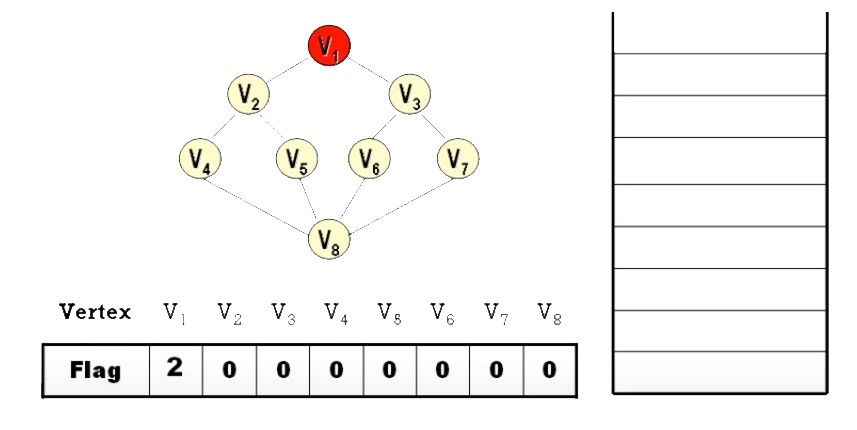
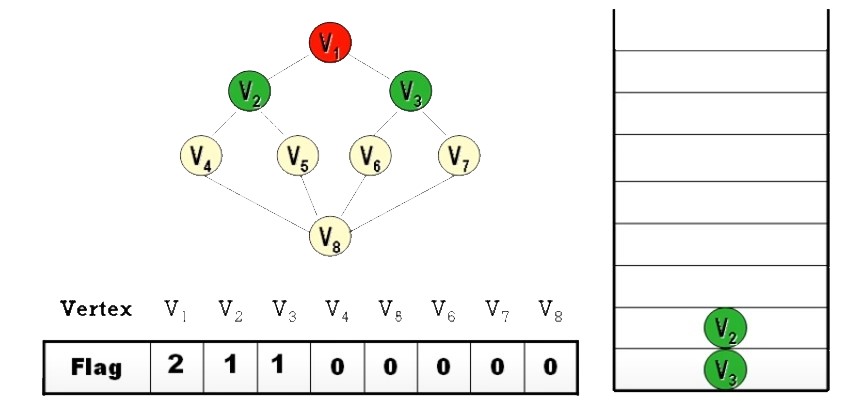
    • Flag = 2：已拜訪 (processed)

Depth-First Traversal

走訪起始頂點 v，然後選擇一個相鄰至 v 且尚未被拜訪過的頂點 w；以w為起始點再做 Depth-First 追蹤。如果從任何已拜訪過的頂點，都無法再拜訪到一個尚未被走過的頂點時，則結束拜訪

包含遞迴應用的概念，因此可利用 Stack 保存走訪過程中間所走過的點

  • Steps:
    1. 選擇一起始拜訪頂點 (可任選) ，將它 Push 到 stack 中
      • 若 Stack 不為空，則
        • 從 Stack 中 Pop 一個頂點 (視為已拜訪頂點)，並將此頂點所有相鄰之其它未拜訪頂點 Push 到 Stack 中。 (重覆執行)
        • 若所有頂點皆已被拜訪過，而 Stack 仍不為空時，則將 Stack 清空
      • 若 Stack 為空，則追蹤程序完成

例:

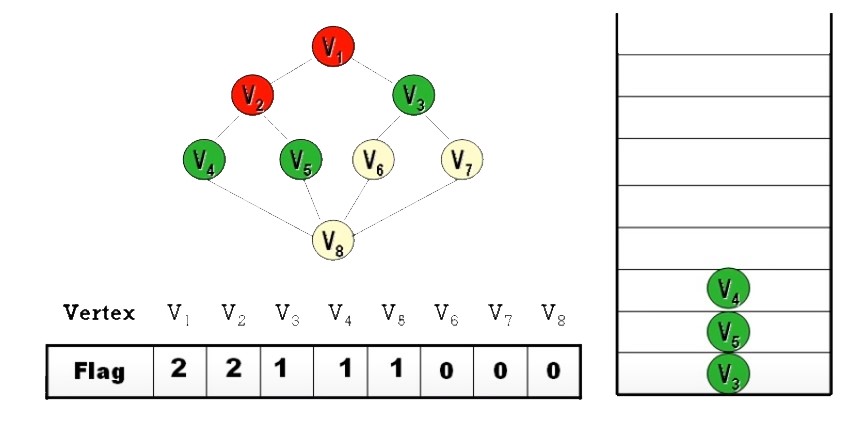
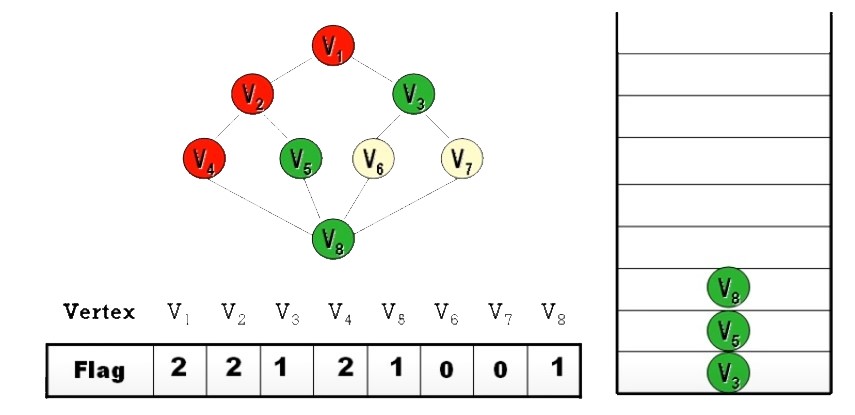
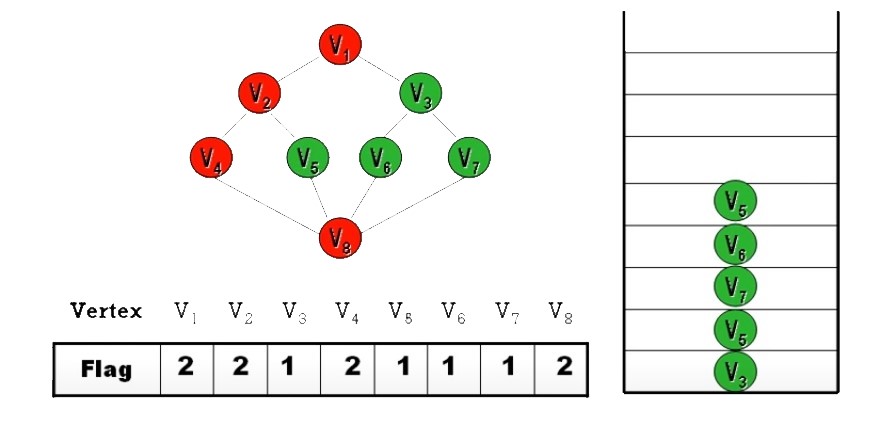
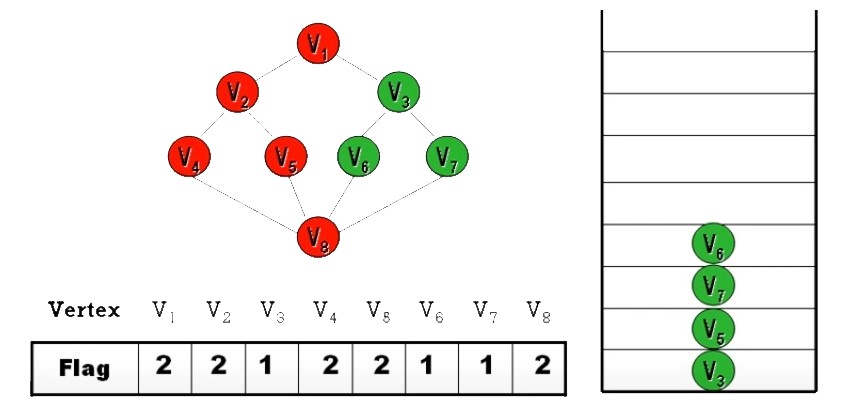
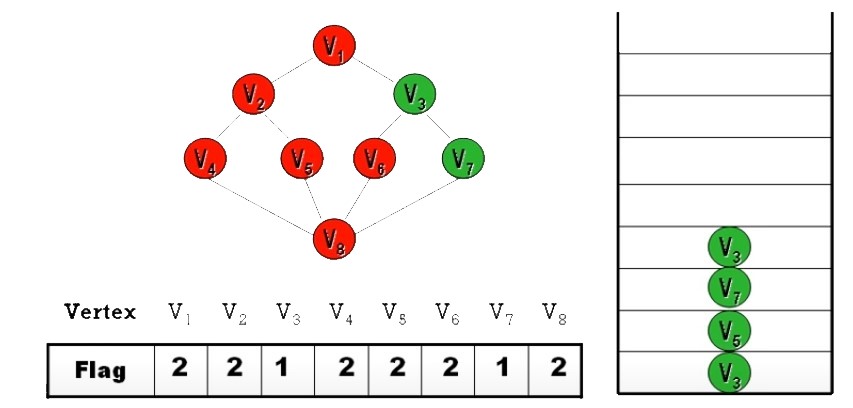
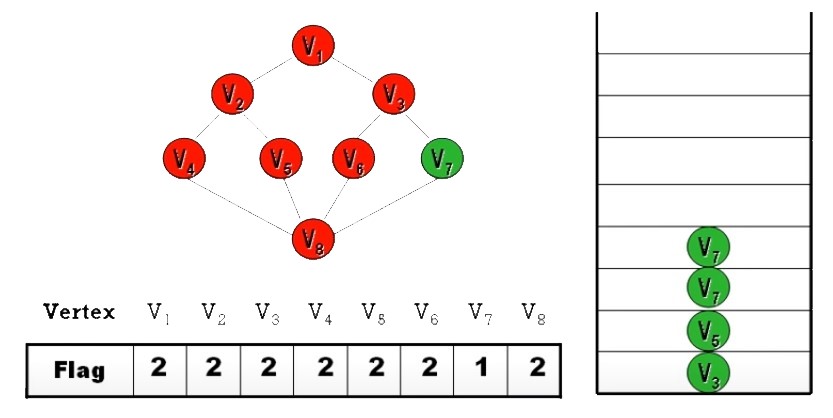
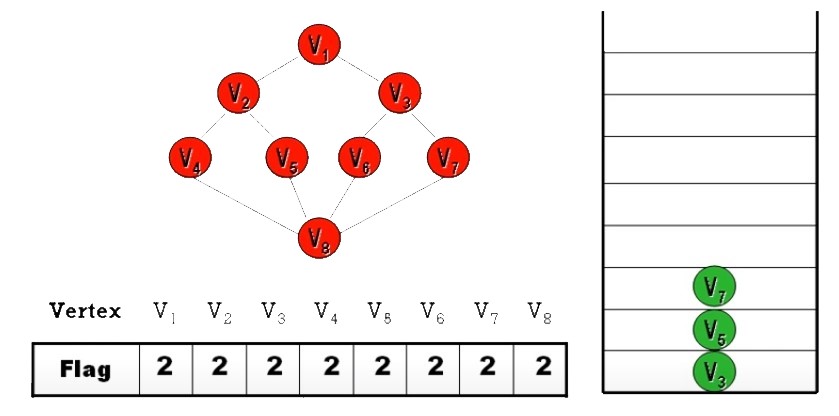
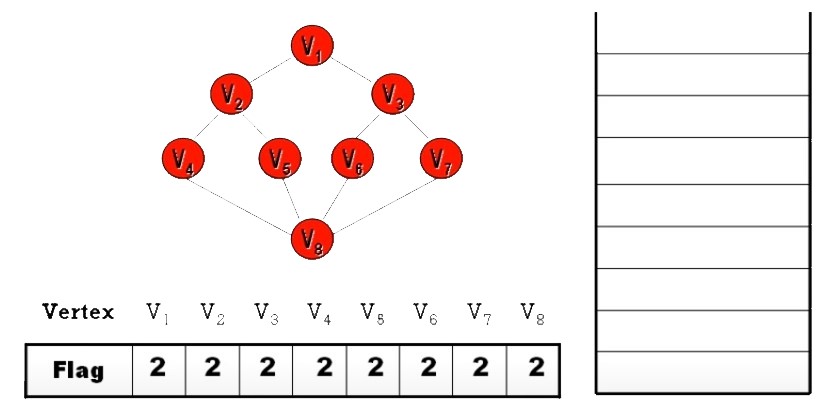
Ans:

  • DFS 之順序並不唯一
    • 起始頂點可任選
    • 每個頂點的分枝路徑可任選
  • 除非規定 “拜訪時，依 Node 編號由小到大拜訪” 才會唯一 (上面答案就是)

例: 承上圖，下列何者不為 DFS 之 Order?

  1. 1, 2, 5, 8, 6, 3, 7, 4
  2. 1, 3, 6, 8, 5, 2, 4, 7
  3. 1, 3, 7, 8, 6, 5, 2, 4
  4. 1, 2, 4, 8, 6, 3, 7, 5
  5. 1, 3, 7, 8, 5, 4, 2, 6

Ans: e

Breadth-First Traversal

由起始頂點 v 開始走訪。所有相鄰至 v 且尚未被拜訪過的頂點，都會在下個步驟裡一一被走訪。而相鄰至這些被走訪頂點且尚未走過的頂點，又將被一一走訪；重複上述，直到無頂點可被拜訪為止

  • Steps:
    1. 選擇一起始拜訪頂點 (可任選) ，將它放入 Queue 中
      • 若 Queue 不為空，則
        • 從 Queue 的前端移出一個頂點 (視為已拜訪頂點)，並將此頂點所有相鄰之其它未拜訪頂點放入 Queue 中。 (重覆執行)
      • 若 Queue 為空，則追蹤程序完成

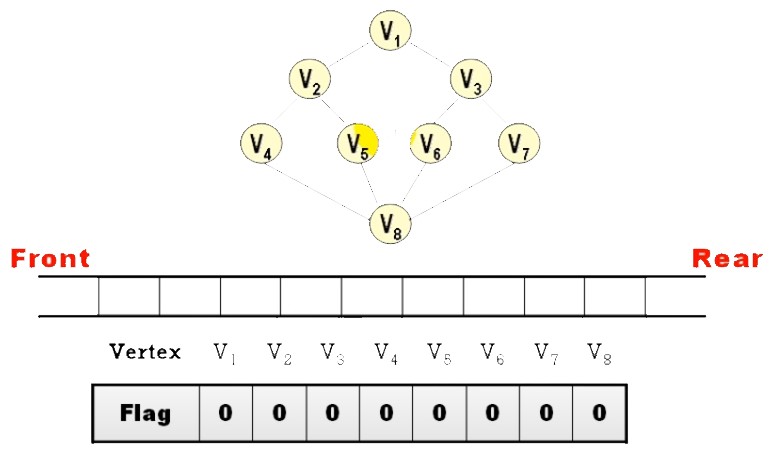
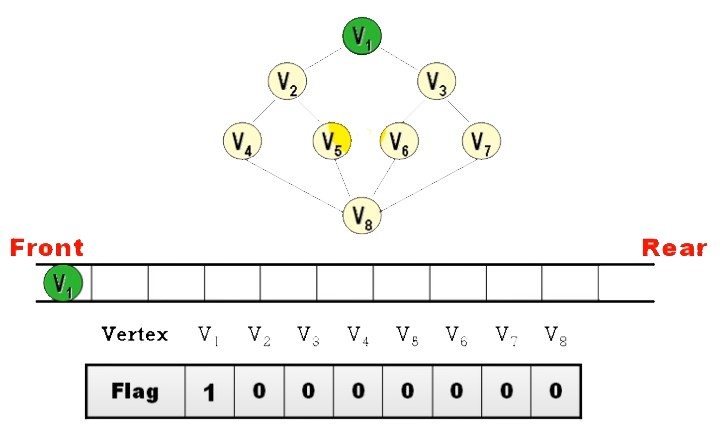
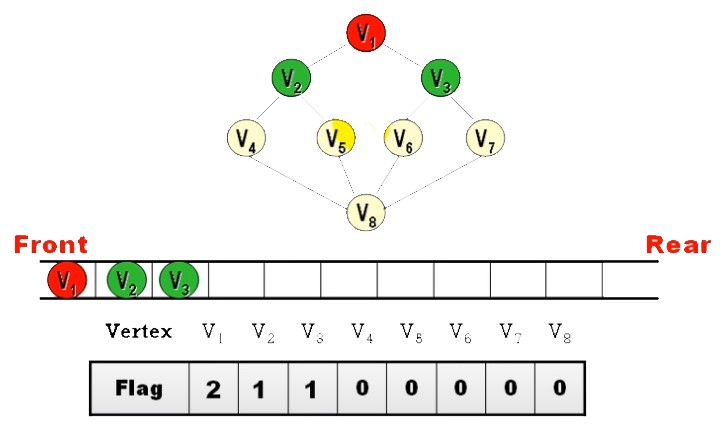
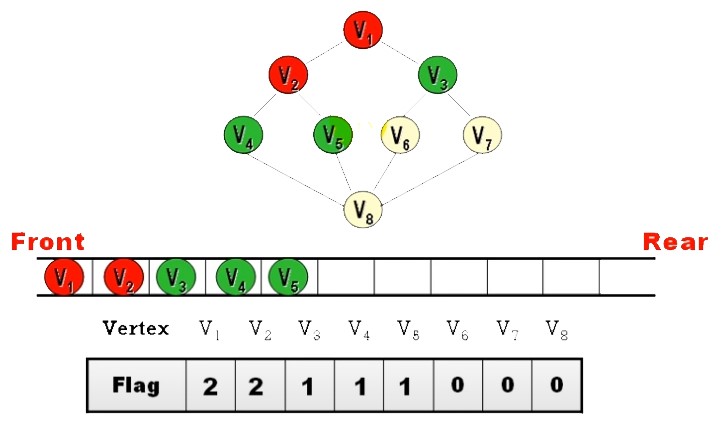
Ans:

  • BFS 之順序並不唯一
  • 除非規定 “拜訪時，依 Node 編號由小到大拜訪” 才會唯一 (上面答案就是)

AOV (Activity On Vertex) Network

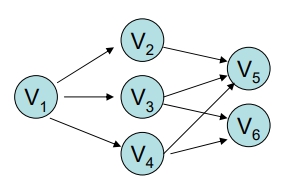
  • 假設 G = <V, E> 為一個 Directed grapth，其中 Vertex 表示工作(Activity)，Edge 表示工作執行之先後次序關係
  • E.g. ，表示 工作必須先於 執行，稱 G 為 AOV Network
  • 應用: 求合理的工作執行順序 ⇒ 即： Topological Order (拓樸順序)

Topological Order (拓樸順序)

給定一個不具 Cycle 的 AOV Network，則可以定出 ≥ 1 組 Vertex (或稱 job ) 的拜訪順序，且此順序須滿足: “若在 AOV Network， 為 的前導，則在此順序中， 必定出現在 之前”

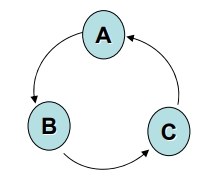
例： 請列出下圖的其中一組 Topological Order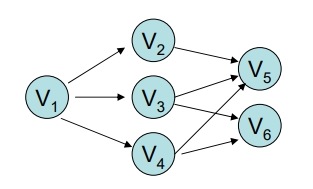

  1. 找出一個無前導的頂點 (Indegree = 0)
  2. 將此頂點輸出，且刪除此點所 Leading-out 之 edge
  3. Repeat 1~2，直到所有 Vertex 已輸出，或剩下的點皆有前導存在
  4. If “不是所有點皆輸出” then “No Topological Order 存在”

Ans:

  • 若 AOV Network 有 cycle，則無 Topological Order。(∵ 無法決定誰先做)
  • 不具 cycle 的 AOV Network，其 Topological Order ≥ 1組。 (不一定唯一)

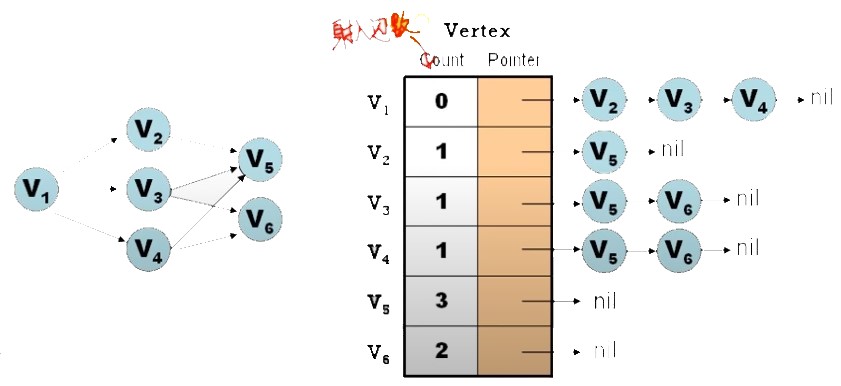
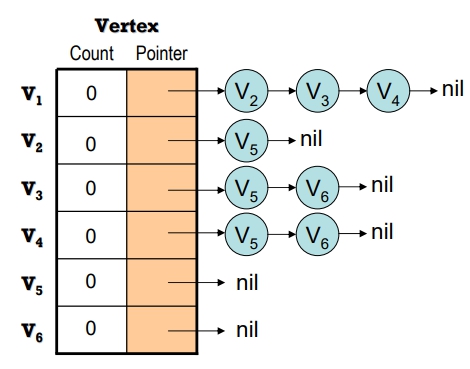
AOV Network 之資料結構表示

做法：

  • 利用 Adjacency List，並在相鄰串列 Vertex[1…n] 中多加一個欄位： count 欄，用以記錄 vertex 的射入邊數 (即：in-degree)
  • 如何實作 “刪除某 vertex 所 Leading-out 之 edge” 的動作？
    • 從該 vertex 的相鄰串列中，找出與之相鄰的其它頂點
    • 將這些頂點的 count 欄之值減1
      • ∵ 刪除某 vertex 所 Leading-out 之 edge = 降低與該 vertex 相鄰之所有頂點的 in-degree 數目。(沒有實質的 “刪除邊” 之動作)

範例：

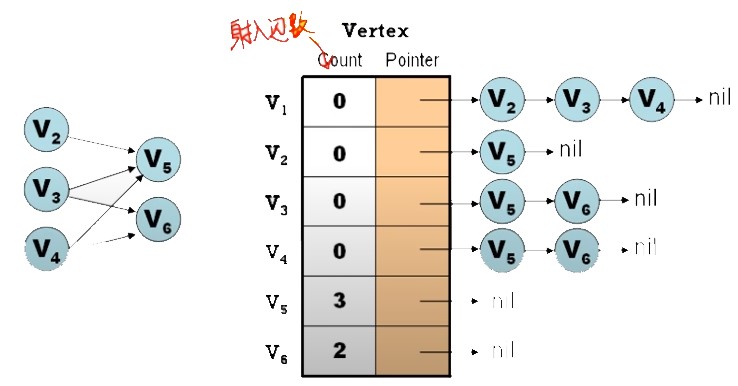
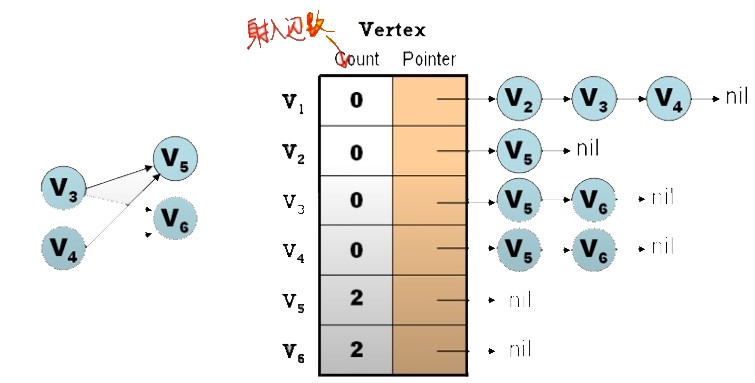
  1. 找出一個無前導的頂點 (Indegree = 0)
  2. 將此頂點輸出，且刪除此點所 Leading-out 之 edge
  3. Repeat 1~2，直到所有 Vertex 已輸出，或剩下的點皆有前導存在
  4. If “不是所有點皆輸出” then “No Topological Order 存在”

\[ ... \]

Ans:

AOE Network

G = (V, E) 有向圖，以 Edge 表示工作 (Activity)，Vertex 表示事件 (Event)，Edge 上具有加權值，表示工作完成所需的時數

  • 事件發生，射出工作 (leading out) 才可以開始執行
  • 所有射入工作完成，事件才會發生

  • 完成此計畫所需之最少(最起碼)的工作時數?
    • 求從 Start → End 事件之最長路徑長度
    • 即: 求 Critical path (臨界路徑)的長度
  • 上圖的可能路徑有(取部份為例):
    • (時數= 18)
    • (時數= 18)
    • (時數= 18)
    • (時數= 18)
    • (時數= 14)
    • (時數= 11)
    • 最長路徑的長度為 18，因此有四條路徑為 Critical path
  • 前例所有的臨界路徑有:
    • (時數= 18)
    • (時數= 18)
    • (時數= 18)
    • (時數= 18)
    • 交集的工作為 ，此即為 Critical Task。若加速此工作，則有助於縮短完成時間。

參考資料

國立聯合大學陳士杰資料結構