Complexity
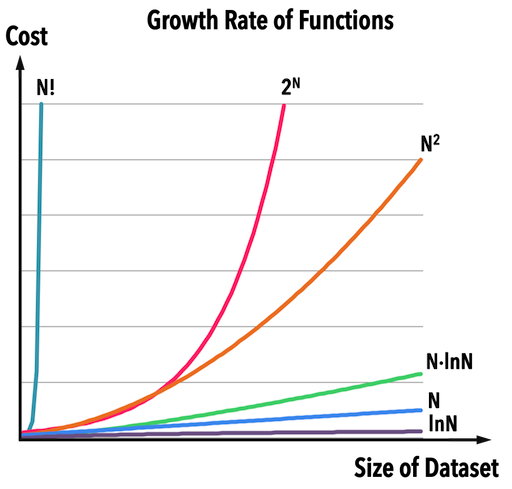
- 研究演算法是為了
正確有效率地解決問題 最有效率的是常數的時間複雜度(
最有效率的是常數的時間複雜度(通常,一個演算法的複雜度必須為\(\Theta(n\lg n)\)或更好,我們才會認為這個演算法能在可忍受的時間內處理輸入大小非常大的範例
),意思其「運算成本與資料量無關」,所以不管資料量多大,保證能夠在「可數(countable)、有限(finite)」的時間內完成
Asymptotic Notation (Order)
在評估演算法之 Complexity 時,常使用 Asymptotic Notation,其概念為:
- 希望能以「簡單的函數」(例如:
等等)來描述 Complexity 的「趨勢」,特別是針對資料量非常大的時候。
Asymptotic Notation 是所有能夠描述演算法趨勢的「函數之集合」,給定:
- n:輸入資料量大小
- 非負函數
:在理想狀況下,程式在電腦中的 指令實際執行次數 - 非負函數
:執行時間的 成長率
以下分別介紹五個 Asymptotic Notation
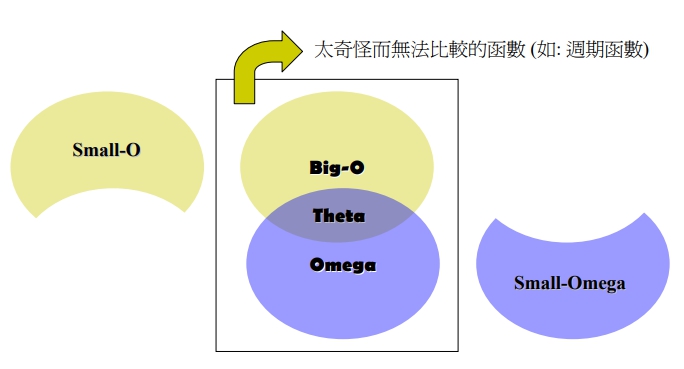
Big-O Notation
一般談論的演算法之複雜度,經常是指 Big-O,因為在估算成本時,最想知道的是「上界(upper bound)」
定義
\[ O(g(n))= \lbrace f(n) 存在兩正數 \:c, n_0 ,並且對於所有 n\geq n_0, 滿足 0\leq f(n) \leq cg(n) \rbrace \]
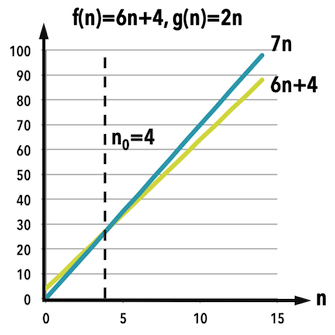
範例
- f(n) = 3n + 2, 則 f(n) = O(n)
f(n) = O(n) if and only if 存在兩正數 c = 4 和 \(n_0\) = 2, 使得 f(n) \(\leq\) c \(\times\) g(n), \(\forall n \geq n_0\)
- 先決定 c 的值,鎖定 f(n) 中的最大項之值( 即: 3n ),c 只要比該項的常數值
大 1即可!!再由 c 去推 \(n_0\) - 3n + 2 \(\leq\) 4n \(\Rightarrow\) n \(\geq\) 2
- f(n) = 5\(n^2\) + 3n + 2,則 f(n) = O(\(n^2\))
f(n) = O(\(n^2\)) if and only if 存在兩正數 c = 6 和 \(n_0\) = 4, 使得 f(n) \(\leq\) c \(\times\) g(n), \(\forall n \geq n_0\)
- 先決定 c 的值,鎖定 f(n) 中的最大項之值( 即: \(5n^2\) ),c 只要比該項的常數值
大 1即可!!再由 c 去推 \(n_0\) - \(5n^2 + 3n + 2 \leq 6n^2 \Rightarrow 3n + 2 \leq n^2 \Rightarrow 取 n_0 = 4\)
Lower bound of f(n)
定義
f(n) = \(\Omega\)(n) if and only if 存在兩正數 c 和 \(n_0\), 使得 f(n) \(\geq\) c \(\times\) g(n), \(\forall n \geq n_0\)
範例
- f(n) = 3n + 2, 則 f(n) = \(\Omega\)(n)
f(n) = \(\Omega\)(n) if and only if 存在兩正數 c = 3 和 \(n_0\) = 任取正數, 使得 f(n) \(\geq\) c \(\times\) g(n), \(\forall n \geq n_0\)
- 先決定 c 的值,鎖定 f(n) 中的最大項之值( 即: 3n ),c 只要與該項的常數值
相同即可!!再由 c 去推 \(n_0\) - 3n + 2 \(\geq\) 3n \(\Rightarrow\) 2 \(\geq\) 0(恒真,故 \(n_0\)可任取)
- f(n) = 5\(n^2\) + 3n - 2,則 f(n) = \(\Omega\)(\(n^2\))
f(n) = \(\Omega\)(\(n^2\)) if and only if 存在兩正數 c = 5 和 \(n_0 = \frac{2}{3}\), 使得 f(n) \(\geq\) c \(\times\) g(n), \(\forall n \geq n_0\)
- 先決定 c 的值,鎖定 f(n) 中的最大項之值( 即: \(5n^2\) ),c 只要與該項的常數值
相同即可!!再由 c 去推 \(n_0\) - \(5n^2 + 3n - 2 \geq 5n^2 \Rightarrow 3n - 2 \geq 0 \Rightarrow 取 n_0 = \frac{2}{3}\)
定義
\[\Theta(g(n))= \lbrace f(n):存在正數 c_1, c_2, n_0,並且對於所有 n\geq n_0,滿足 0\leq c_{1}g(n)\leq f(n) \leq c_{2}g(n) \rbrace\]
表示
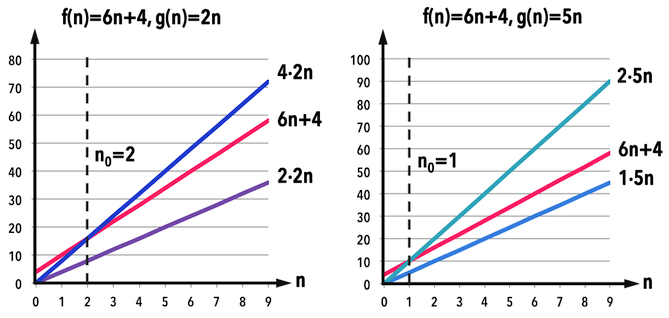
根據定義,既然係數
- 由此可以確認,
是多個函數的「集合」。
以上情況可以推廣至所有的多項式(polynomial),以
或者 表示
範例
f(n) = 3n + 2, 則 f(n) = θ(n)
- f(n) = θ(n) if and only if 存在三正數 \(c_1\) = 3 , \(c_2\) = 4 和 \(n_0\) = 2 , 使得 \(c_1\) × g(n) ≤ f(n) ≤ c2 × g(n), \(\forall n ≥ n_0\)
- 用先前決定 O 與 Ω 中 c 值的方式分別得到 \(c_1\) 與 \(c_2\) 即可!!再由 \(c_1\) 與 \(c_2\) 去推 n
- 3n + 2 ≤ 4n (用f(n) ≤ \(c_2\) × g(n)來找) \(\Rightarrow\) n ≥ 2
- If f(n) = O(g(n)) 且 f(n) = Ω(g(n)), 則f(n) = θ(g(n))
\(O, \Omega 與\Theta 的關係\)
以 f(n) = 3n + 2 與 f(n) = 5\(n^2\) + 3n + 2 為例:
- 3n + 2:
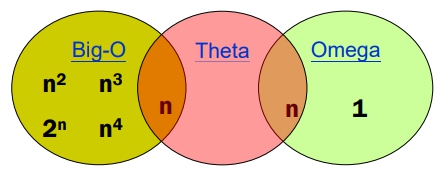
- 5\(n^2\) + 3n + 2:
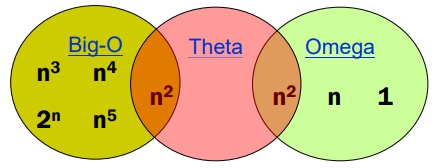
Big-Theta(
定義
f(n) = o(g(n)) if and only if 對任何正數 c 會存在一個正數 \(n_0\), 使得 f(n) < c \(\times\) g(n), \(\forall n \geq n_0\)
與 Big-O 的比較:
- f(n) = O(g(n)) if and only if 存在兩正數 c 和 \(n_0\), 使得 f(n) \(\leq\) c \(\times\) g(n), \(\forall n \geq n_0\)
- 例如:
- 2n = \(o(n^2)\)
- 2\(n^2 \neq 0(n^2)\), 但是 2\(n^2\) = O(\(n^2\))
f(n) = \(\omega\)(g(n)) if and only if 對任何正數 c 會存在一個正數 \(n_0\), 使得 f(n) > c \(\times\) g(n), \(\forall n \geq n_0\)
與 Omega 的比較:
- f(n) = \(\Omega\)(g(n)) if and only if 存在兩正數 c 和 \(n_0\), 使得 f(n) \(\geq\) c \(\times\) g(n), \(\forall n \geq n_0\)
- 例如:
- \(5n^2 + 3n + 2 = \omega (n)\)
- \(5n^2 + 3n + 2 = \neq \omega(n^2), 但是 5n^2 + 3n + 2 = \Omega(n^2)\)
題外話
如果我們說一個執行時間是