使用 Limit 來決定 Order
Limit

- 邏必達法則 (L’ Hospital Rule)
先備工具
常用的數學式子
- \(\log \log n = \log (\log n)\)
- \({\log}^kn = (\log n)^k\)
- \(a = b^{\log_ba}\)
- \(\log_cab = \log_ca + \log_cb\)
- \(\log_c\frac{a}{b} = \log_ca - \log_cb\)
- \(\log_ba^n = n\log_ba\)
- \(\log_ba = \frac{\log_ca}{\log_cb}\)
- \(\log_ba = \frac{1}{\log_ab}\)
- \(\log_b\frac{1}{a} = \log_ba^{-1} = -\log_ba\)
- \(a^{\log_bc} = c^{\log_ba}\)
練習
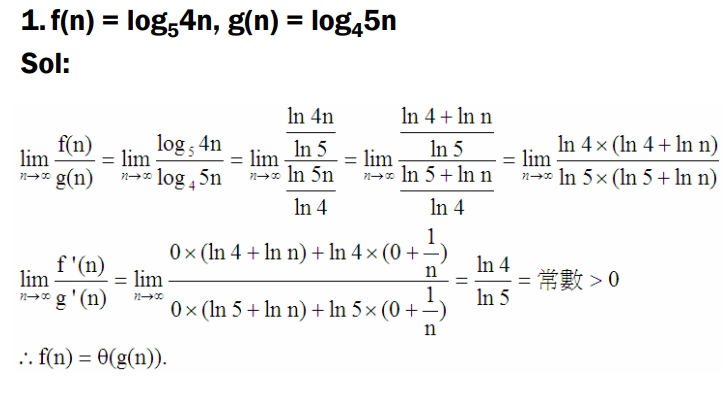




Note
- Log 的底和 Complexity 無關
- 若 log f(n) = o(log g(n)),
可保証f(n) = o(g(n)) - 若 log f(n) = ω(log g(n)),
可保証f(n) = ω(g(n)) - 若 log f(n) = θ(log g(n)),
不可保証f(n) = θ(g(n))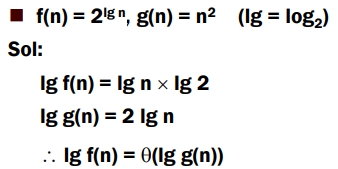
- 若 log f(n) = o(log g(n)),
- 兩函數的 Complexity 有可能無法比較 (Ex: 週期函數)