Recursion 的複雜度分析

分析步驟：

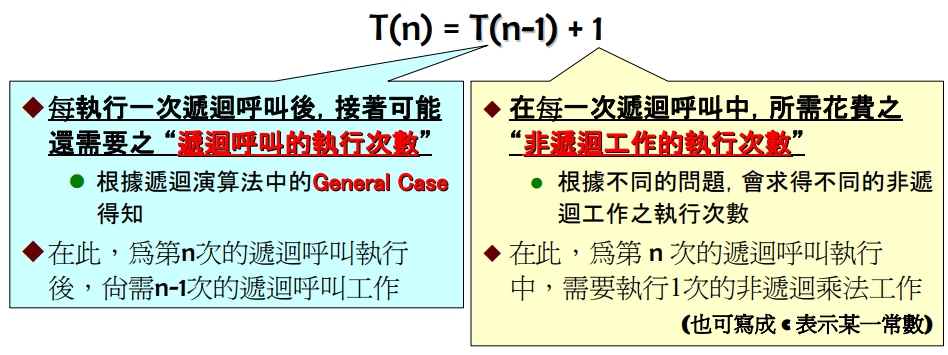
1. 找出遞迴演算法的遞迴方程式 T(n) 來表達該演算法的執行次數
2. 解這個遞迴方程式來求出該演算法的時間複雜度

例子

Factorial

Fibonacci

如何解遞迴方程式

通常在討論遞迴演算法時，我們常會一起將這些演算法的遞迴方程式列出。因此，本篇假設遞迴方程式已給定，主要議題則設定在如何解遞迴方程式

• 遞迴方程式的解法與使用時機:

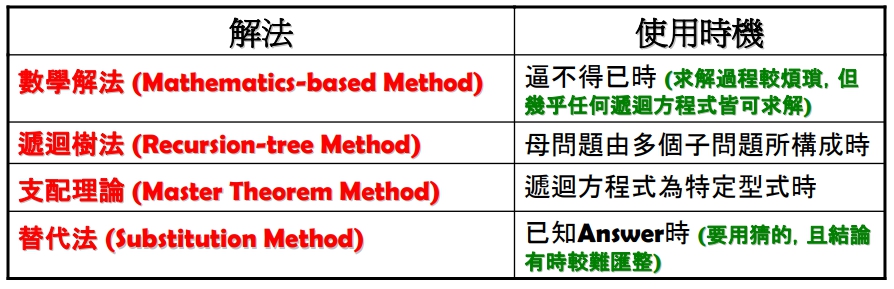
下面來深入探討個別解法

數學解法

直接將遞迴方程式以遞迴的觀念由最末項往前求解，然後整理出答案

範例 1

範例 2

遞迴樹法

• 適用於母問題由多個子問題所構成
• 使用一個樹狀結構表示遞迴演算法則在執行過程被遞迴呼叫的情況，這個樹狀結構稱為遞迴樹。其中:
  • Node: 存放遞迴關係式所相對應之子問題的 Cost
  • Degree: 子問題的數目
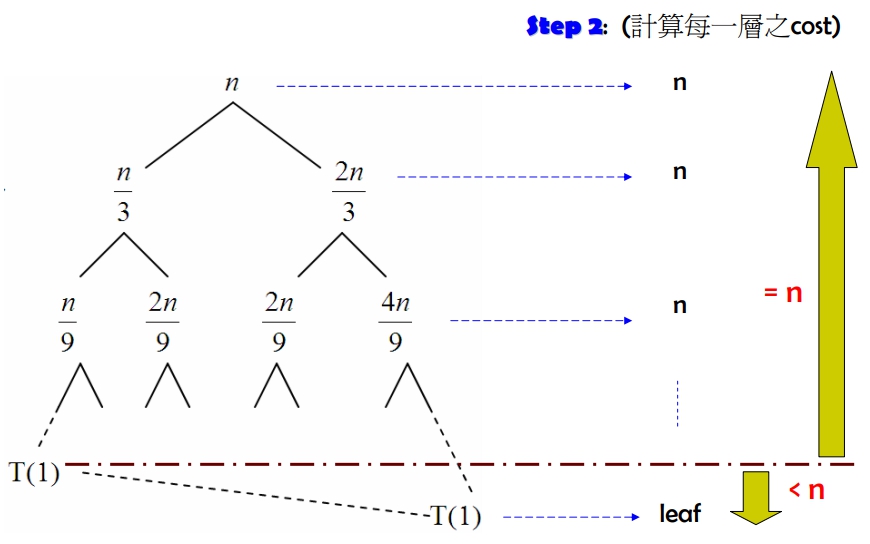
• 遞迴樹法的三個步驟:
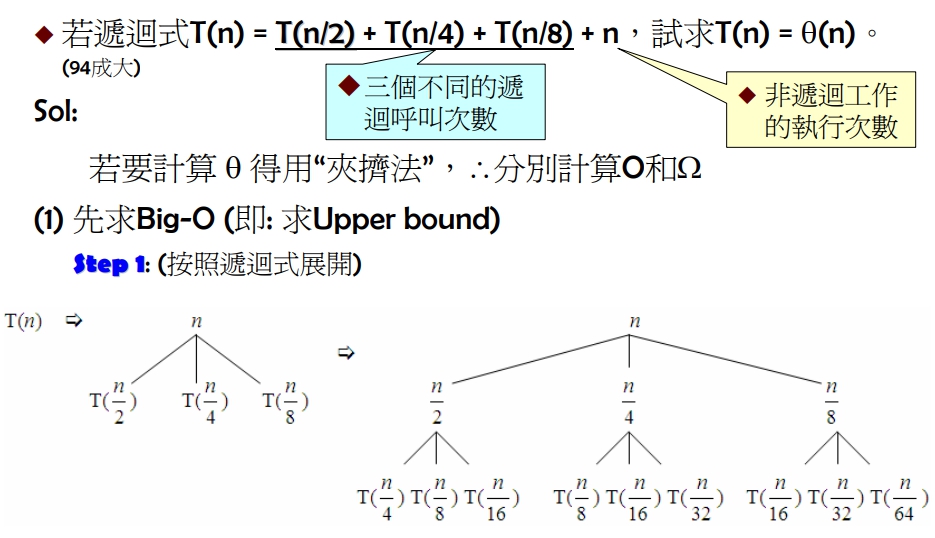
  • 按照遞迴方程式展開
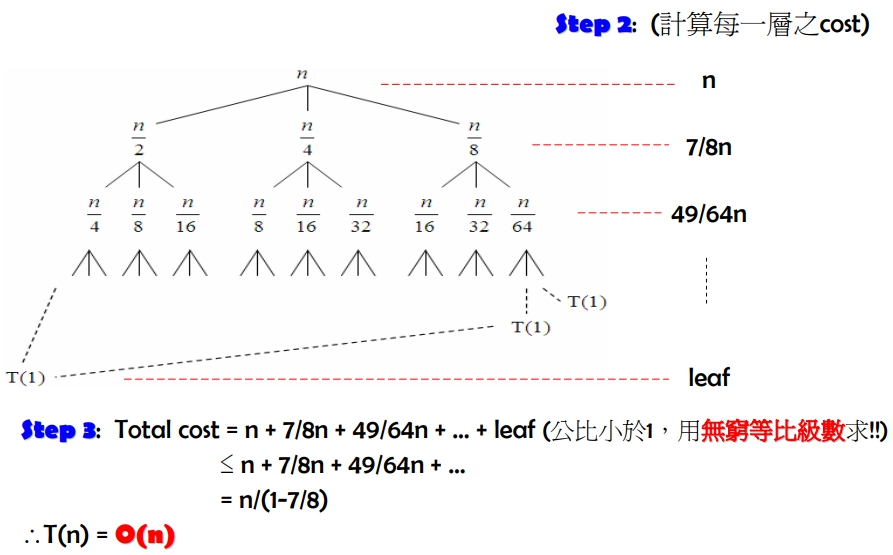
  • 對每一層的所有子問題之 cost 加總，得到每一層之 cost
  • 加總每一層的 cost，以得到 total cost，即為答案
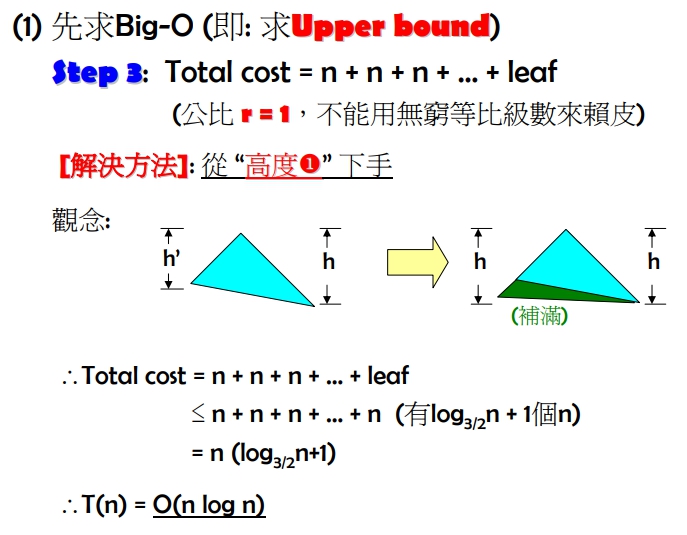
• 通常只能求出 Big-O 或 Ω，若要計算 θ 得用“夾擠＂法

範例 1

範例2

支配理論方法

• 當遞迴方程式具有某種特定型式時適用
• 【精神】讓 f(n) 和 \(n^{log_ba}\) 比大小

範例 1

範例 2

替代法

• 適用於檢驗某個候選解答是否為此遞迴演算法的正確解，而不適用於求遞迴方程式的解答
• 使用步驟:
  1. 利用猜測、觀察或匯整的方式，找出遞迴方程式的解(很麻煩)
  2. 利用數學歸納法証明此解是正確的
• 由於利用此方法求解遞迴方程式，最難的地方就是如何去猜出、觀察出或匯整出遞迴方程式的解。所以一般只適合當已有候選解時，用來驗証該解是否正確，也就是為了避開第一個步驟。

範例 1

範例 2

參考資料

國立聯合大學陳士杰資料結構