Heap Sort
Heapsort 的演算法分為兩大步驟:
- 將資料轉換為
heap資料結構(遞增排序用max-heap, 遞減排序選擇min-heap)。 - 逐步取出最大/最小值,並與最後一個元素置換。具體步驟如下:
- 交換 heap 的 root 與最後一個 node,縮小 heap 的範圍(排序一筆資料,故 heap 長度 -1)。
- 更新剩下的資料,使其滿足 heap 的特性,稱為 heap ordering property。
- 重複前兩個步驟,直到 heap 中剩最後一個未排序的資料。
Heapsort(堆積排序)可以看作是 selection sort 的變形,同樣會將資料分為 sorted pile 與 unsorted pile,並在 unsorted pile 中尋找最大值(或最小值),加入 sorted pile 中。 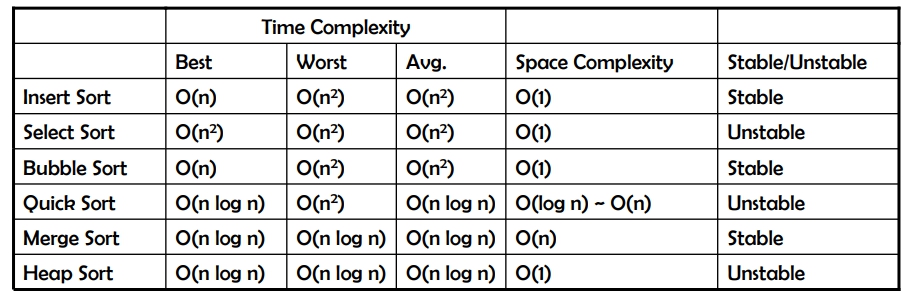
Binary Heap
Binary Heap 有兩項基本特徵:
特徵一
Binary Heap 之結構可以視作 Complete Binary Tree 。
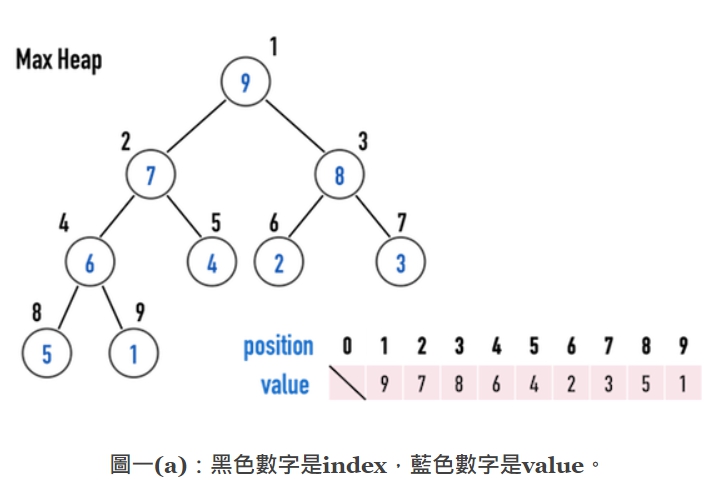
- 如圖一(a),數值1~9,一共有9個元素,按照 Complete Binary Tree 之順序規則,填滿位置1~9,以 index(1)~index(9) 表示。
這樣的優點是方便尋找「parent-child」之關係,以 index(i) 的 node 為例:
- 其 left child 必定位在 index(2i)
- 其 right child 必定位在 index(2i+1)
- 其 parent 必定位在 index(⌊i/2⌋)
以圖一(a)中位於 index(3) 之 node(8) 為例:
- 其 left child 為 index(6) 之 node(2);
- 其 right child 為 index(7) 之 node(3);
- 其 parent 為 index(1) 之 node(9)。
特徵二
若將位於 index(i) 之 node 視為 subtree 之 root ,那麼,可將此 Binary Heap 分為兩類:
- Max Heap:在每一個 subtree 中, root 之「數值」要比兩個 child 之「數值」還要大,見圖一(a):
- value(i) > value(2i)
- value(i) > value(2i+1)
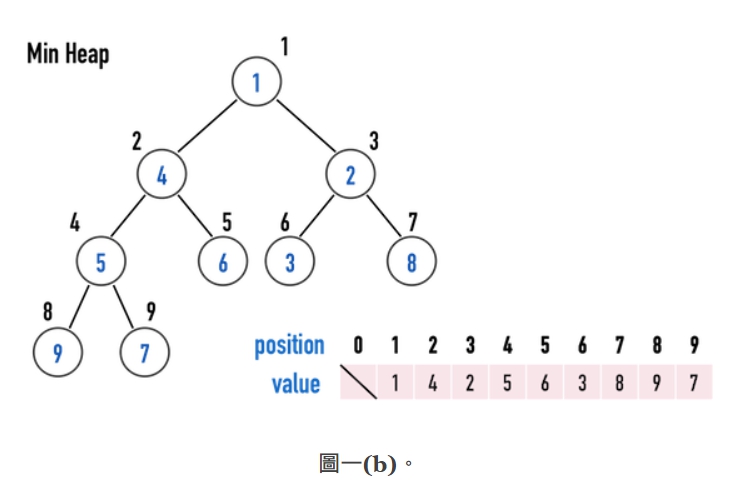
- Min Heap:在每一個 subtree 中, root 之「數值」要比兩個 child 之「數值」還要小,見圖一(b):
- value(i) < value(2i)
- value(i) < value(2i+1)
Heap 相關操作與分析
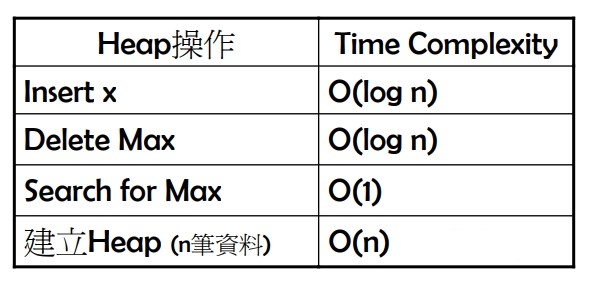
Heap 提供下列 2 個運作:
Insert
- 將 x 置於 Last Node 之後
- x 向上挑戰父點(即: 與父點的值比大小),直到發生下列任一狀況為止:
- 挑戰失敗
- 無父點
Time 之分析
- Insert x 後,x 的最大移動距離為
從 leaf 到 root,即為樹高,又 Heap 為 Complete B.T. - ∴ 當有 n 個 nodes 時,樹高為: \(\lceil \log_2(n+1)\rceil\)
∴ Insert 之 Time 為 O(log n)
Delete
- 移走 Root 的元素
- 將 Last Node x 刪除並置於 Root 位置
- 從 Root 往下調整成 Max-Heap (Max-Heap 調整方法: 跟較大的兒子交換)
Time 之分析
- Step 1 與 Step 2 的動作只花 O(1) (常數時間)
- Step 3 花費時間較多,故以此為主
- Last Node x 的最大移動距離為
從 Root 到 leaf,即為樹高,又 Heap 為 Complete B.T. - ∴ 當有 n 個 nodes 時,樹高為: \(\lceil \log_2(n+1)\rceil\)
- Last Node x 的最大移動距離為
∴ Delete 之 Time 為 O(log n)
Heap 的建立方式
分為以下兩種:
- Top-Down
- Bottom-Up (Siftdown)
Top-Down
連續執行Insert的動作,每一個步驟執行後均維持 Max-Heap
Bottom-Up (Siftdown)
- 先將資料建成Complete B.T.
- 從 “Last Parent” 往 “Root” 方向,逐次調整每棵子樹成為 Max-Heap
Stpe 1 之所以將之建成 Complete B.T.,是因為真正在寫程式時,可用 Array 儲存,會較易搜尋子節點及父節點
建立 Heap 花費時間
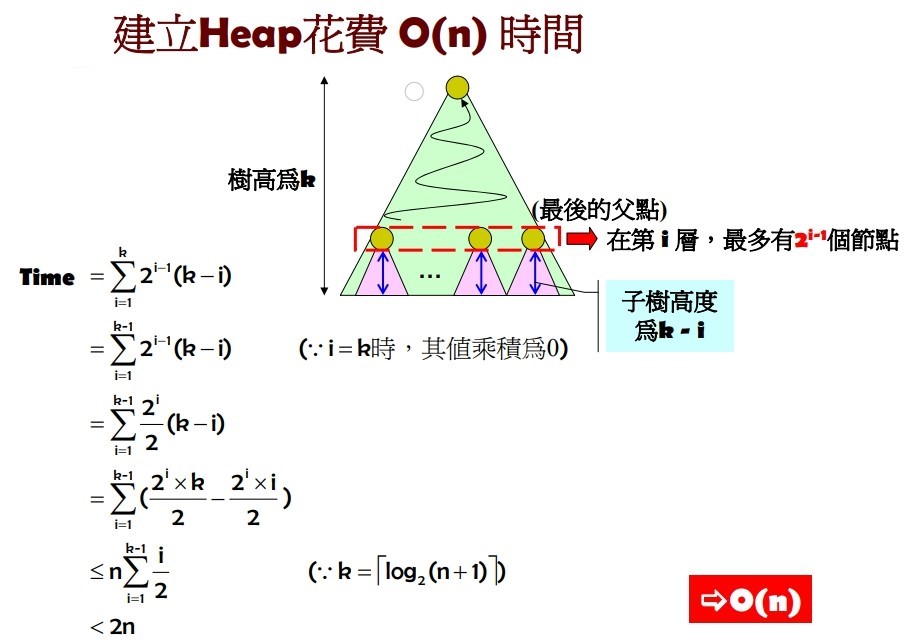
可以參考 UMD 演算法課程 Lecture note 的分析。
後記
- 同樣資料,用 Top-Down 及 Bottom-up 所建立出來的 Max-Heap
不一定相同 - 通常 Bottom-up 的實際執行速度較
快!! (但兩者的 Time Complexity 相同)
heapsort 步驟說明
而 heapsort 主要分為兩個部分:
- Heapify:將資料先以“Bottom-up” 的方式建立 Max-Heap
- Sorting:執行 n-1 回合的 “Delete Max” 動作
程式碼
HeapSortview rawdef heapify(unsorted, index, heap_size): largest = index left_index = 2 * index + 1 right_index = 2 * index + 2 if left_index < heap_size and unsorted[left_index] > unsorted[largest]: largest = left_index if right_index < heap_size and unsorted[right_index] > unsorted[largest]: largest = right_index if largest != index: unsorted[largest], unsorted[index] = unsorted[index], unsorted[largest] heapify(unsorted, largest, heap_size) def heap_sort(unsorted): n = len(unsorted) # 建立 binary heap(heapify) for i in range(n // 2 - 1, -1, -1): heapify(unsorted, i, n) # Sorting(sift down) for i in range(n - 1, 0, -1): unsorted[0], unsorted[i] = unsorted[i], unsorted[0] heapify(unsorted, 0, i) return unsorted if __name__ == "__main__": user_input = input("Enter numbers separated by a comma:\n").strip() unsorted = [int(item) for item in user_input.split(",")] print(heap_sort(unsorted))
時間複雜度
Avg. / Worst / Best Case: O(n log n)
- 建立 Max-Heap 會花費 O(n) 時間
- 需執行 n-1 回合的 Delete Max 動作,而每一次的 Delete Max 動作需花費 O(log n) 時間 ⇒ 共花費 O(n log n)
∴ 整個 Heap-Sort 花費 O(n) + O(n log n) ≅ O(n log n) 時間
空間複雜度
Heap-Sort 是 in-place sort ∴ Space Complexity: Θ(1)
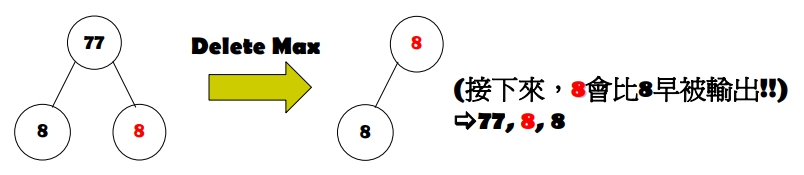
Unstable
有一組資料: 8, 8, 77,其 Max-Heap 如下。若進行 Heap Sort 時,執行一回合的 Delete Max: