Recursion
遞迴的基本概念就是:
To solve a problem, solve a subproblem that is a smaller instance of the same problem, and then use the solution to that smaller instance to solve the original problem.
最後可以整理出兩個重點:
- Each recursive call should be on a smaller instance of the same problem, that is, a smaller subproblem.
- The recursive calls must eventually reach a base case, which is solved without further recursion.
簡單來說：
- 決定基本情況 (Base Case)
- 此 base case 即為遞迴的終止條件
- 決定一般情況 (General case)
- 産生遞迴呼叫的指令碼，即遞迴關係式
- 將上述兩種情況寫入演算法
Procedure 遞迴程式名(參數) { if (Base case) return(結果); ……//達到終止條件時結束遞迴，需要時回傳結果 else General case; ……//利用general case執行遞迴呼叫，需要時加上return }
議題
- 階乘(Factorial;n!)
- 費氏數(Fibonacci Number)
- 兩數之最大公因數 (Greatest common divisor; G. C. D.)
- 二項式係數 (Binomial Coefficient;或稱組合問題 “Combination of n objects”)
- Ackerman’s Function
- 迴文(palindrome)
- 河內塔問題(Tower of Hanoi)
- 排列問題(Permutation)
遞迴常見的課題：
- 寫一個Algorithm (or Program)
- 追蹤一個Recursion Algorithm (找結果、呼叫次數)
階乘(Factorial;n!)
定義
階乘(n!) = 1 × 2 × 3 × … ×(n-1) × n
解法
- 數學表示式:
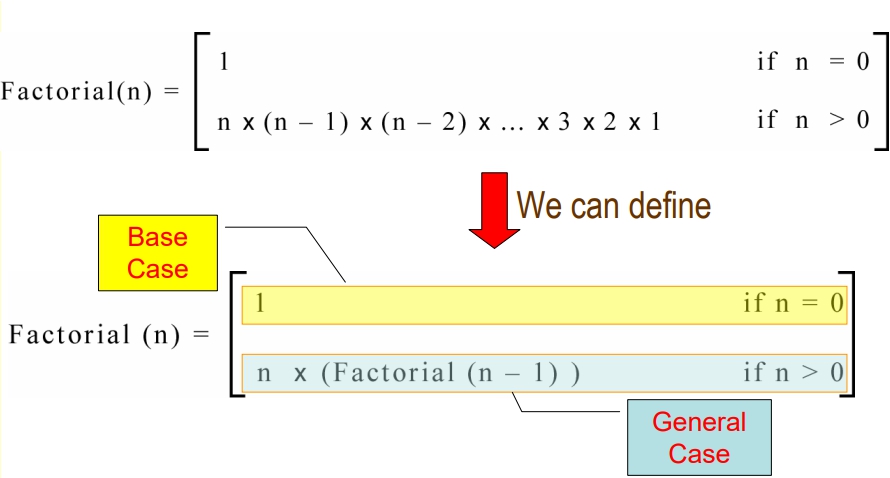
- pseudocode:
Input: 所要求算的階乘數値n Output: n! 結果回傳 Procedure Factorial(int n) begin if (n = 0) return 1; else return (n× Factorial(n-1)); end - Factorial(3) = ? 呼叫了幾次函數？
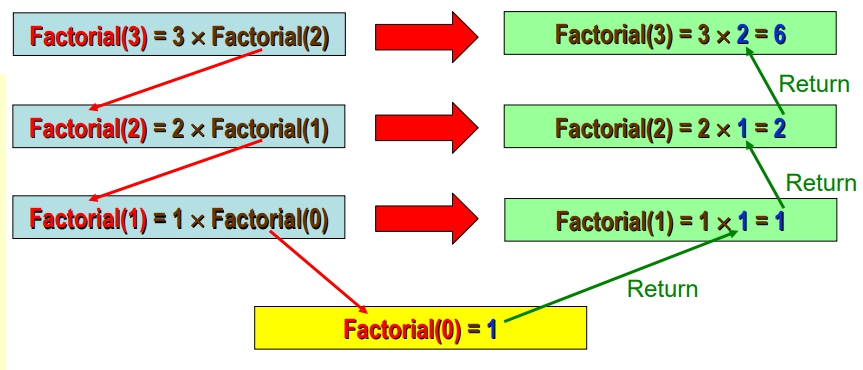呼叫了 4 次 (含Factorial(3))，計算結果為 6 ※ Factorial(n) 會被呼叫幾次? 呼叫 n+1 次 - Iterative Factorial Algorithm 的 pseudocode
Input: 所要求算的階乘數値n Output: n! 結果回傳 Procedure Factorial(int n) begin i = 1; factN = 1; loop (i ≤ n) factN = factN * i; i = i +1; end loop return factN; end - python code
def factorial(num: int) -> int: if num < 0: raise ValueError("Number should not be negative.") return 1 if num in (0, 1) else num * factorial(num - 1)
費氏數(Fibonacci Number)
定義
| n | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 1 | 1 | 2 | 3 | 5 | 8 | 13 | 21 | 34 | 55 |
解法
- 數學表示式:
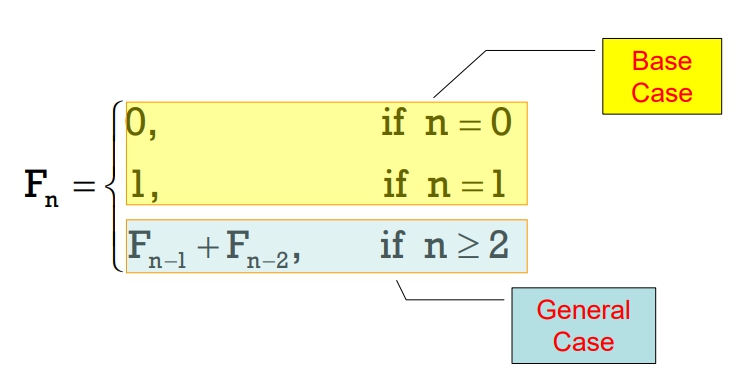
- pseodocode
Input: 費氏數値num Output: 回傳Fibonacci number結果 Procedure Fib(int num) begin if (num is 0 OR num is 1) //Base Case return num; else return (Fib(num-1) + Fib(num-2)); end - Iterative Fibonacci Number Algorithm pseodocode
Input: 費氏數値num Output: 回傳Fibonacci number結果 Procedure Fib(int n) begin if (num is 0 OR num is 1) return num; else begin Fa = 0,Fb = 1; for(i = 2 to n) = 2 to n) Fc = Fa + Fb; Fa = Fb; Fb = Fc; end for; return Fc; end if; end - python code
""" This program calculates the nth Fibonacci number in O(log(n)). It's possible to calculate F(1_000_000) in less than a second. """ import sys def fibonacci(n: int) -> int: if n < 0: raise ValueError("Negative arguments are not supported") return _fib(n)[0] # returns (F(n), F(n-1)) def _fib(n: int) -> tuple[int, int]: if n == 0: # (F(0), F(1)) return (0, 1) # F(2n) = F(n)[2F(n+1) − F(n)] # F(2n+1) = F(n+1)^2+F(n)^2 a, b = _fib(n // 2) c = a * (b * 2 - a) d = a * a + b * b return (d, c + d) if n % 2 else (c, d)class Fibonacci: def __init__(self, N=None): self.fib_array = [] if N: N = int(N) self.fib_array.append(0) self.fib_array.append(1) for i in range(2, N + 1): self.fib_array.append(self.fib_array[i - 1] + self.fib_array[i - 2]) elif N == 0: self.fib_array.append(0) print(self.fib_array) def get(self, sequence_no=None): """ >>> Fibonacci(5).get(3) [0, 1, 1, 2, 3, 5] [0, 1, 1, 2] >>> Fibonacci(5).get(6) [0, 1, 1, 2, 3, 5] Out of bound. >>> Fibonacci(5).get(-1) [0, 1, 1, 2, 3, 5] [] """ if sequence_no is not None: if sequence_no < len(self.fib_array): return print(self.fib_array[: sequence_no + 1]) else: print("Out of bound.") else: print("Please specify a value") if __name__ == "__main__": print("\n********* Fibonacci Series Using Dynamic Programming ************\n") print("\n Enter the upper limit for the fibonacci sequence: ", end="") try: N = int(input().strip()) fib = Fibonacci(N) print( "\n********* Enter different values to get the corresponding fibonacci " "sequence, enter any negative number to exit. ************\n" ) while True: try: i = int(input("Enter value: ").strip()) if i < 0: print("\n********* Good Bye!! ************\n") break fib.get(i) except NameError: print("\nInvalid input, please try again.") except NameError: print("\n********* Invalid input, good bye!! ************\n") import doctest doctest.testmod()
兩數之最大公因數 (Greatest common divisor; G. C. D.)
定義
省略。
解法
- 利用輾轉相除法，如下圖所示：
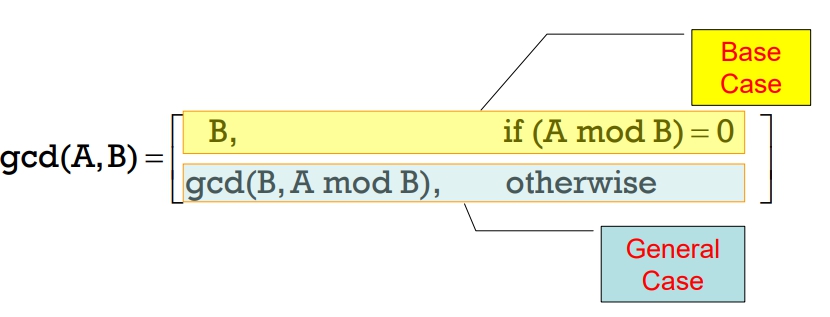
- pseudocode
Input: 輸入二個整數A與B Output: 傳回A與B的最大公因數 Procedure gcd(int A, int B) begin if (A mod B = 0) //Base Case return B; else return gcd(B, A mod B); end - PS. 不用考慮 A < B 的問題。因為假如 A < B ：gcd(A, B) = gcd(B, A)，等於前面多 call 一次遞迴
二項式係數 (Binomial Coefficient;或稱組合問題 “Combination of n objects”)
定義
組合問題的公式如下：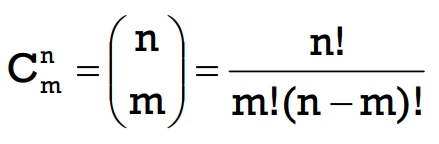 
解法
本題解法思路不需要去管，因為最後遞迴關係式式數學家推導出來的：
數學表示式：
pseudocode
Input: 輸入二項式的n與m Output: 傳回二項式計算結果 Procedure Bin(int n, int m) begin if (n=m or m=0) //Base Case return 1; else return (Bin(n-1, m) + Bin(n-1, m-1)); end
Ackerman’s Function
定義
省略。
解法
- 數學表示式
- pseudocode
Input: 輸入Ackerman(M, N) Output: 傳回Ackerman(M, N)計算結果 Procedure Ackerman(M, N) begin if (M=0) //Base Case return N+1; elif (N=0) return Ackerman(M-1, 1) else return Ackerman(M-1, Ackerman(M, N-1)) end - 追蹤遞迴
河內塔問題(Tower of Hanoi)
定義
河內塔也是個經典的 Recursion 問題。因為此屬簡單問題所以簡單介紹。 河內塔目標是把 n 個盤子從 A 柱移動到 B 柱(如下圖 n = 5)，且遵循以下兩個規則:
- 一次只能移動一個盤子
- 較小的盤子必須在較大的盤子上面
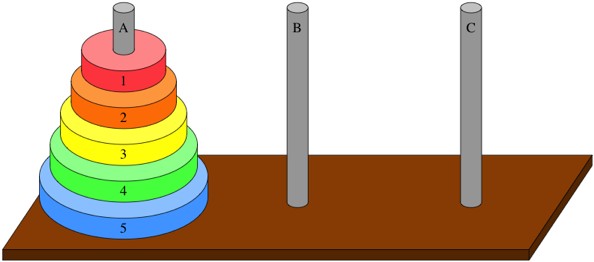
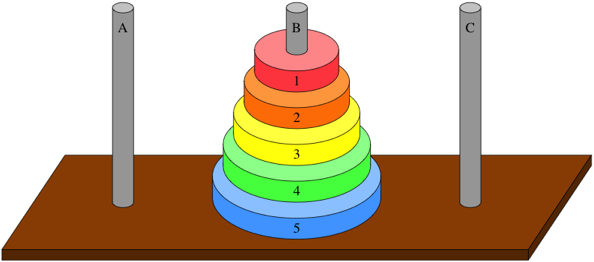
傳說在亞洲某個地方盛傳一個傳說，如果把當地 64 個盤子成功移動到另一個柱子，世界末日即將到來！
解法
因為很簡單所以直接說解法了。 觀察:
- n = 1，只需要一次(直接把盤子放到B柱)
- n = 2，需要三次(如下圖)
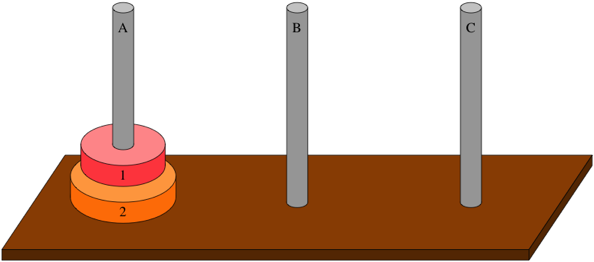
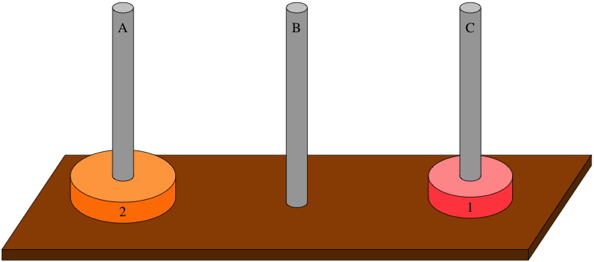
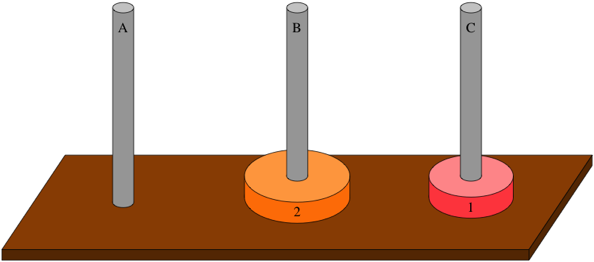
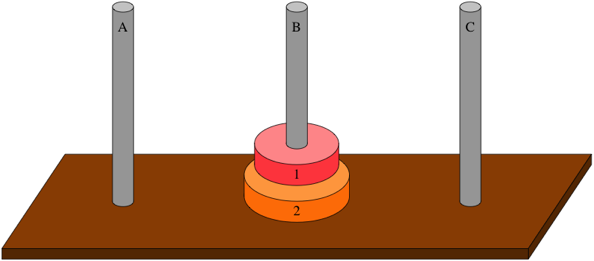
- n = 3，需要 3+1+3 次(把 2 個盤子從 A 柱放到 C 柱，移動最大盤從 A 到 B 柱，把 2 個盤子從 C 放到 B 柱)
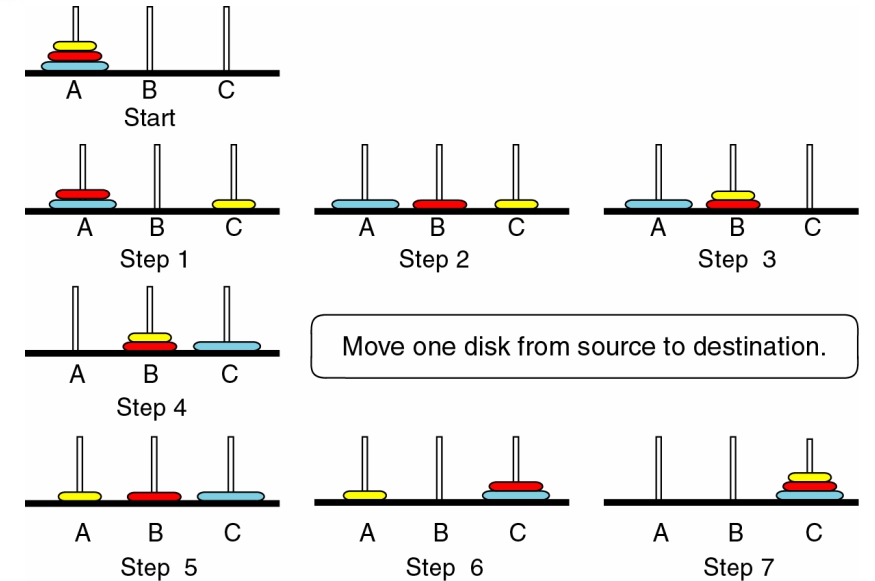
數學表示式:
- Base Case: if n = 1, 移動一次
- General Case: when n >=2, 解問題按照下列三步驟:
- 遞迴解決子問題n-1移動次數
- 移動最大盤
- 遞迴解決子問題n-1移動次數
- Recursive Tower of Hanoi Algorithm pseudocode
Input: n個盤子，三根柱子(A, B, C) Output: 移動過程 Procedure Towers(int n, char A, char C, char B) begin if (n > 0) Towers(n Towers(n-1, A, B, C); 1, A, B, C); print(“Move disk”, n, “from”, A, “to”, C); Towers(n Towers(n-1, B, C, A); end python code
def moveTower(height,fromPole, toPole, withPole): if height >= 1: moveTower(height-1,fromPole,withPole,toPole) print("moving disk from",fp,"to",tp) moveTower(height-1,withPole,toPole,fromPole)moveTower(3,"A","B","C")
時間複雜度
T(n) = T(n-1) + 1 + T(n-1) = 2T(n-1) + 1 = 2[2T(n-2) + 1] + 1 = 4T(n-2) + 3 = ... =
由上可知一個遞迴演算法會包含兩個部份：
- 遞迴呼叫的執行次數 : 2T(n-1)
- 非遞迴工作的執行次數 : 1
回到剛剛說世界末日的故事，移動64個盤子需要
次，假設每秒可以移動一個盤子，則大概需要5845億年來移動，還沒到那時太陽的壽命已經消耗殆盡了！
Permutation (排列問題)
定義
給予 a，b，c 三個字元，請印出所有的 Permutation。
- 共有3! = 6 種排列
解法
- 數學表示式
- pseudocode
void perm(list[ ], int i, int n) // 此函式可產生從 list[i] 至 list[n] 的元素排列 { if (i==n) // 當 list[ ] 中的所有元素排列完畢，即：終止條件 { for (j=1; j<=n; j++) print(list[j]); // print list內排列好的結果 } else // 當 list[ ] 中的元素尚未排列完畢，即：遞迴關係式 { for(j=i; j<=n; j++) { swap(list[i], list[j]); // 讓某個字元當頭(第j個字元當頭) perm(list[ ], i+1, n); // 從第i字元後的其他字元，自己去做排列 swap(list[i], list[j]); // 將list陣列還原 } } }
Recursion 與 Non-recursion 的比較
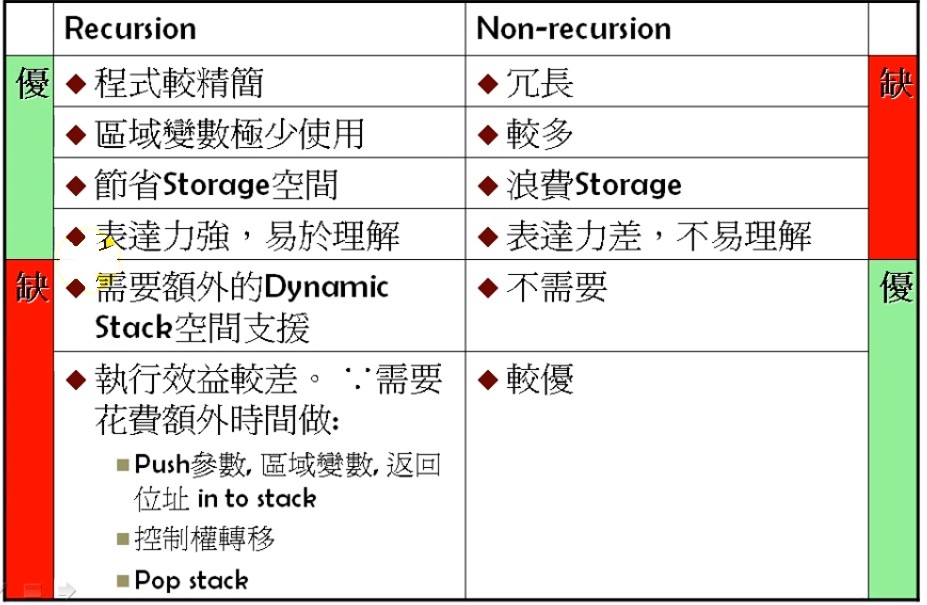
上圖說明:
區域變數指的是程式碼而非執行時期的Storage空間指的是程式碼的儲存空間而非執行時期的
Memoization 優化
考慮 Fibonacci 數列:
- If n is 0 or 1, return n
- Otherwise, return fibonacci(n-1) + fibonacci(n-2)
當 n = 5 時, the computer makes 15 calls:
隨著 n 越來越大，fibonacci(30) 在遞迴時 call 了 fibonacci(2) 超過 50 萬次。 > 所以我們可以實做一個 lookup table 紀錄算過的 fibonacci(input)，當然這個 table 要有效率像是 hash table 擁有- if n == 0 or 1, return n
- if n in the table, return the table's value for n
- Otherwise
- 計算 fibonacci(n-1) + fibonacci(n-2)
- 儲存 result 在 table
- return result
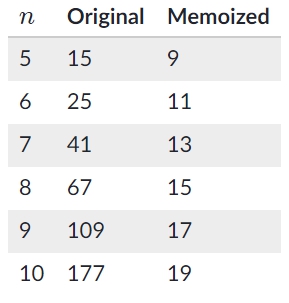
如上表所示，隨著 n 越來越大 function call 以指數增加，但是佔用的 space 卻是線性增加。
Bottom-up
有時候改善 recursive algorithm 最有效的方法就是不使用 recursion。
在這個 Fibonacci numbers 例子中，一個 iterative 技巧叫做 bottom-up approach 可以同時節省 time 和 space。當使用 bottom-up approach 時，會先解決子問題然後使用部份解去得出最終解。
- time complexity:
- space complexity:
since it only remembers three numbers at a time.
以下是pseudocode:
- if n == 0 or 1, return n
- Otherwise
- Create variable twoBehind to remember the result of (n-2) and initialize to 0
- Create variable oneBehind to remember the result of (n-1) and initialize to 1
- Create variable result to store the final result and initialize to 0
Repeat (n-1) times:
- Update result to the sum of twoBehind plus oneBehind
- Update twoBehind to store the current value of oneBehind
- Update oneBehind to store the current value of result
- return result
初探 Dynamic programming
上述的 Memoization 和 bottom-up 都是使用了 dynamic programming 策略。
當一個問題具有* *optimal substructure 和 overlapping subproblems** 特性時，Dynamic programming 則可以被使用。
- Optimal substructure: the optimal solution to the problem can be created from optimal solutions of its subproblems.
- fib(5) can be solved with fib(4) and fib(3)
- Overlapping subproblems: whenever a subproblem is solved multiple times.
- fib(5) made multiple calls to the typically recursive fib(3) and fib(2)
總結
當以下的問題有任何一個為 當以下的問題有任何一個為 no，則不該使用遞迴來設計演算法 用遞迴來設計演算法:
- 問題的演算法或資料結構本身是否就具備 問題的演算法或資料結構本身是否就具備遞迴的特性?
- 使用遞迴求解問題是否能 使用遞迴求解問題是否能更簡化或是更易了解?
- 使用遞迴求解問題是否能在 使用遞迴求解問題是否能在可接受的時間或記憶體空間限制下完成?