AVL Tree
前言 : Binary Search Tree 的效益
- 當 B.S.T. 建立之後,可以用來搜尋資料。因此,由平均比較次數來決定其效益
- 若平均比較次數愈低,則效益愈高
- 例:
- 成功搜尋的平均比較次數:
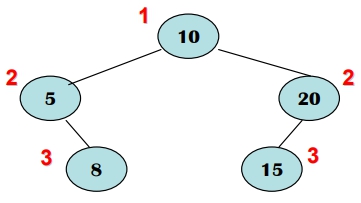
- 成功搜尋的平均比較次數:
- 結論: 不考慮加權値或加權値皆相同的情形下
- 愈
平衡的 Binary Search Tree,其平均比較次數愈小,Big-O ≈O (log n) - 愈
偏斜的 Binary Search Tree,其平均比較次數愈大,Big-O ≈O (n)
- 愈
- 在
靜態的環境下,一般 Binary Search Tree 的建構方法可以有較充裕的時間將欲搜尋的所有資料建構成較平衡的 Binary Search Tree,以提升後續資料搜尋時的效率 - 然而,若是在
動態的環境下,資料可以隨時Insert / Delete。此時,一般 Binary Search Tree 的建構方法會産生Skewed Binary Tree,導致資料搜尋的效率變差 (即:O (n)) - ∴ 面對動態資料,需要
AVL Tree讓 Tree 的高度均維持在高度平衡的情況
AVL Tree (高度平衡樹)
定義
為一個 Height Balance 的 Binary Search Tree,可以為空,若不為空,則滿足:
- |
| ≤ 1,其中 與 為左、右子樹的高度 - 左右子樹亦是 AVL Tree (∴ AVL Tree 也有遞迴的特性)(前題:不考慮加權値或加權値皆相同的情形下)
範例
- 下列 Binary Search Tree 何著為 AVL Tree?
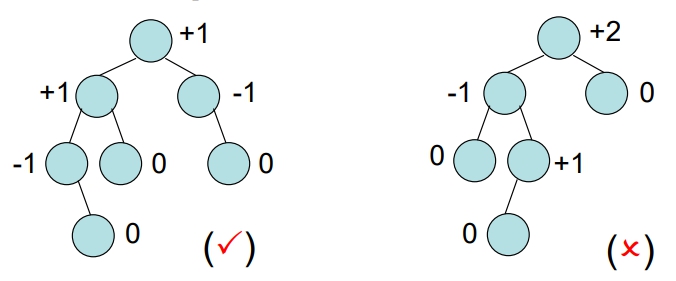
- 下列 Binary Tree 是否為 AVL Tree?
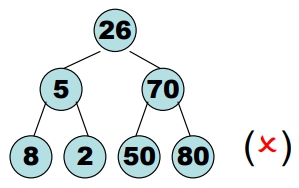
8 > 5, 違反了 Binary Search Tree 的條件,∴ 不是 AVL Tree
AVL Tree 不平衡的情況
Balance Factor (平衡因子)of a node:- B.F. =
- 在 AVL Tree 中,所有節點的 B.F. 只有三種値:
-1 , 0 , +1
- B.F. =
建構 AVL Tree 的過程中,當插入一個新的節點時,可能會造成以下四種不平衡的情況:
LL 不平衡
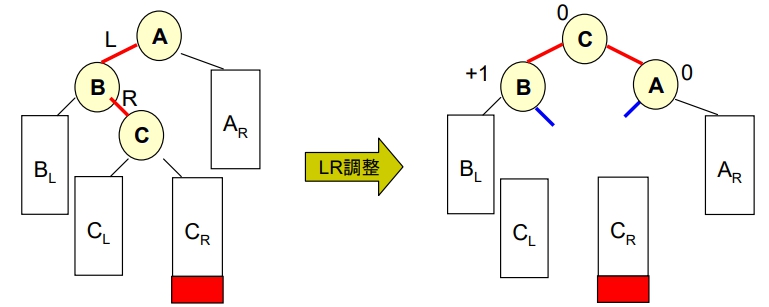
LR 不平衡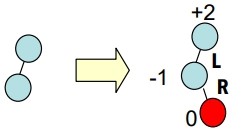
RL 不平衡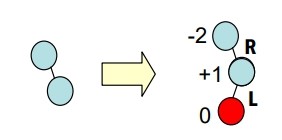
RR 不平衡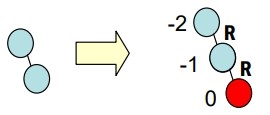
以下 AVL Tree 插入新節點後,會産生何種不平衡?
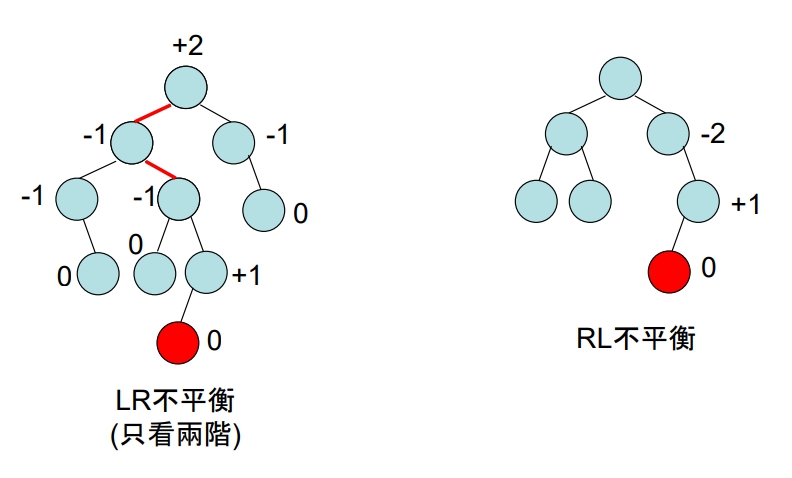
AVL Tree 不平衡情況的調整方式
- 原則:
- 由於四種不平衡情況會牽渉到三個節點,且三個節點內存放的値會有
小、中、大三種不同的資料。故調整時,三個節點的中間値往上拉,小的値放左,大的値放右( 依據 B.S.T. 的特性 ) - 調整後,若産生沒有父親的子樹,則以二元搜尋樹插入資料的方式來判斷該放哪裡
- 由於四種不平衡情況會牽渉到三個節點,且三個節點內存放的値會有
範例
- 若有以下四種不平衡的情況,該如何調整:
LL 不平衡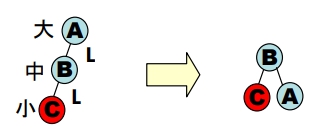
LR 不平衡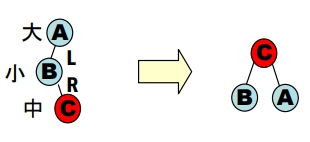
RL 不平衡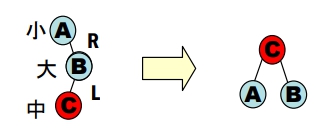
RR 不平衡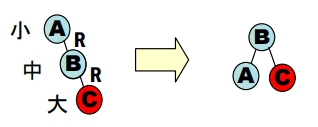
- 若插入資料時發生以下二種情況,該如何調整:
Case 1: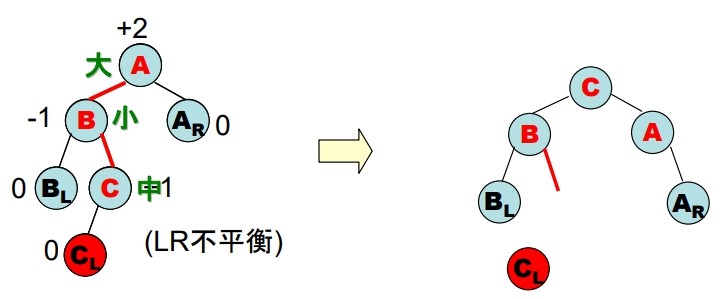
調整後會產生
孤兒節點,此時就利用 B.S.T insert 方法即可Case 2: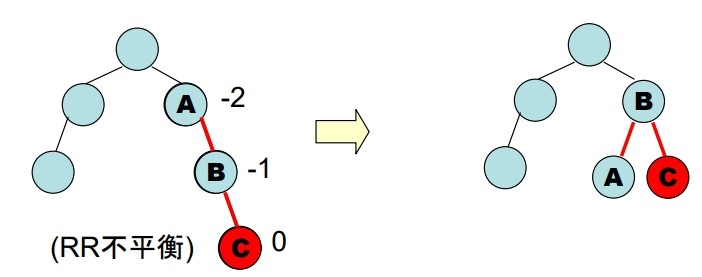
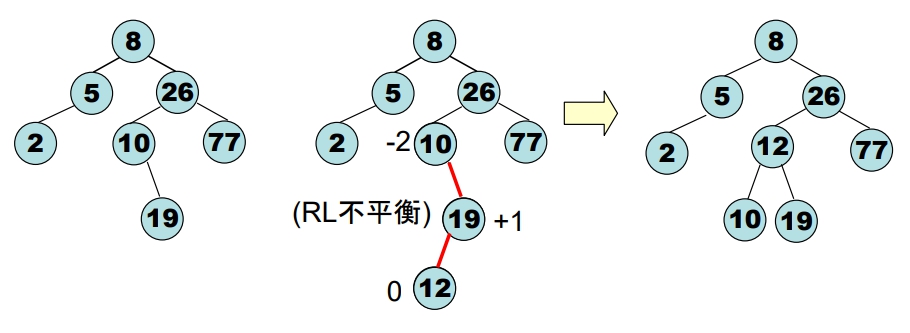
- 給予下列數字,請建立AVL Tree: 5, 26, 77, 2, 8, 10, 19, 12
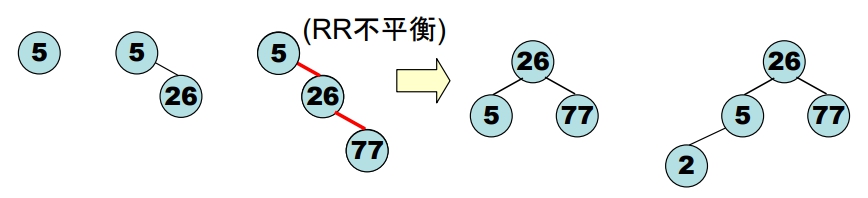
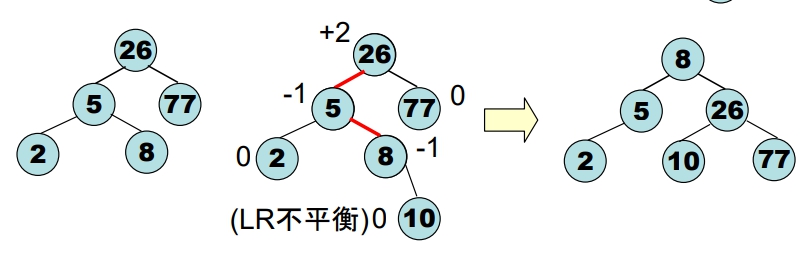
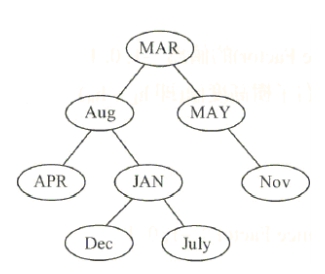
- 下列英文月份的 AVL Tree,若插入 “Feb” 之結果為何? (順序:A < B < C < … < Z )
 Ans:
Ans: 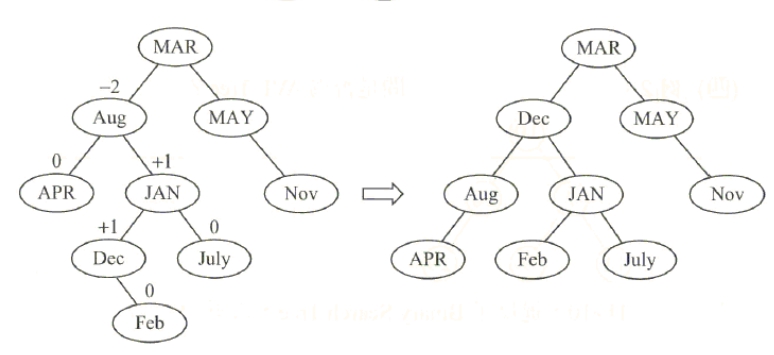
定理
形成高度 h 的 AVL Tree,所須要的最少節點個數為:
範例
- 形成高度為 3 的AVL Tree
- 所需的最少節點個數為 4
畫法: 每一個非葉節點的高度皆差 1
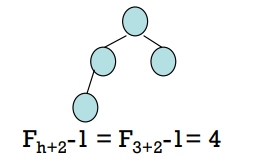
- 所需的最多節點個數為 7
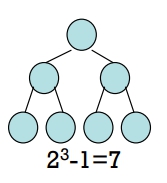
- 所需的最少節點個數為 4
一個 AVL Tree 有 15 個節點,則:
- 最大高度為 5 ( 用最少的點撐出最大的高度 )
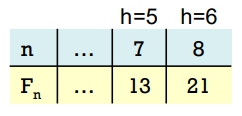
- 最小高度為 4 ( 完整二元樹 )
- 最大高度為 5 ( 用最少的點撐出最大的高度 )
下圖新增節點後
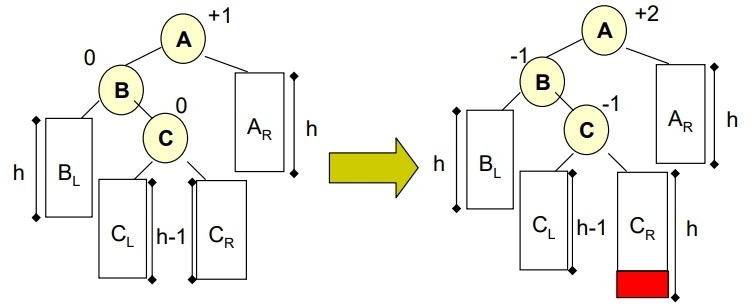 如何調整成 AVL Tree?
如何調整成 AVL Tree?
Ans: