Graph Storage Structures

發表於 Disqus：
文章字數： 2.3k 所需閱讀時間 ≈ 4 分鐘
  • 若要在系統中表示一個圖形，需要儲存兩個集合：
    • 圖形的頂點 ( Vertices )
    • 圖形的邊 （ Edges or arcs )
  • 常用的表示方式：
    • Adjacency Matrix ( 相鄰矩陣 )
    • Adjacency List ( 相鄰串列 )
    • Multiple Adjacency List ( 相鄰多元串列 )
    • Index Array ( 索引陣列 ) # Adjacency Matrix (相鄰矩陣) ## 無向圖 G = (V, E) 為一無向圖，|V| = n。宣告一個 n × n 的二維矩陣 A，其中： \[\begin{equation} A[i, j] = \begin{cases} 0, & if \; (V_i, V_j) \notin E \\ 1, & if \; (V_i, V_j) \in E \end{cases} \end{equation}\]

範例：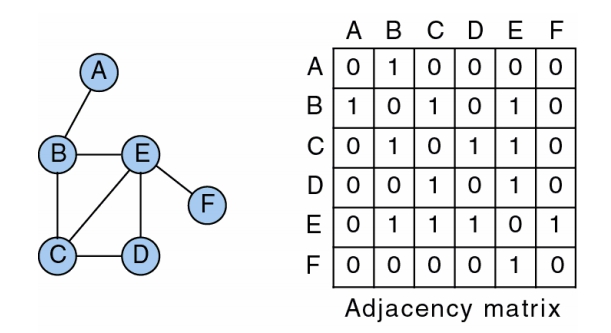

特質

此 Matrix 必為對稱 (Symmetric)

∵ 無向圖中，，∴ A[i, j] = A[j, i] 儲存時可用上三角或下三角陣列

運作

  • 判斷邊 是否存在?
    • 做法：檢査 A[i, j] 的値是否為 1
    • 時間複雜度： O(1)
  • 求頂點 的分枝度?
    • 做法：求第 i 列或第 i 行之元素値總和
    • 時間複雜度： O(n) (∵ 需用一個迴圈)
  • 求圖形的邊數?
    • 做法： \[\begin{equation} e = \sum_{i=1}^n \frac{D_i}{2} = \sum_{i=1}^n \sum_{j=1}^n \frac{A[i, j]}{2} \end{equation}\]
    • 時間複雜度：

有向圖

G = (V, E) 為一有向圖，|V| = n。宣告一個 n × n 的二維矩陣 A，其中： \[\begin{equation} A[i, j] = \begin{cases} 0, & if \; (V_i, V_j) \notin E \\ 1, & if \; (V_i, V_j) \in E \end{cases} \end{equation}\]

範例： (以 Out-degree 為主)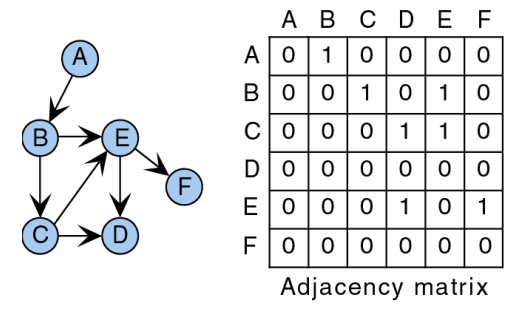

圖中列為 Outdegree，行為 Indegree

特質

此 Matrix 不一定是對稱 (Symmetric)

∵ 有向圖中， 存在，不見得 也會存在

運作

  • 判斷邊 是否存在?
    • 做法：檢査 A[i, j] 的値是否為 1 (同無向圖)
    • 時間複雜度： O(1)
  • 求頂點 的出分枝度與入分枝度? (若矩陣是以 Out-degree 為主)
    • 做法：
      • Out-degree：求第 i 列之元素値總和
      • In-degree：求第 i 行之元素値總和
    • 時間複雜度： O(n) (∵ 需用一個迴圈)
  • 求圖形的邊數?
    • 做法： \[\begin{equation} e = \sum_{i=1}^n D_i^{Out} = \sum_{i=1}^n D_i^{In} = \sum_{i=1}^n \sum_{j=1}^n A[i,j] \end{equation}\]
    • 時間複雜度：

Adjacency List (相鄰串列)

無向圖

若 G = (V, E) 為一無向圖，|V| = n 且 |E| = e，則需使用 n 條相鄰串列與一個 Size 為 n 的一維矩陣 A[1, …, n]，其中 A[i] 所存放的是頂點 i 的相鄰串列，此串列中毎個 Node 皆記録著與頂點 i 相鄰之其它頂點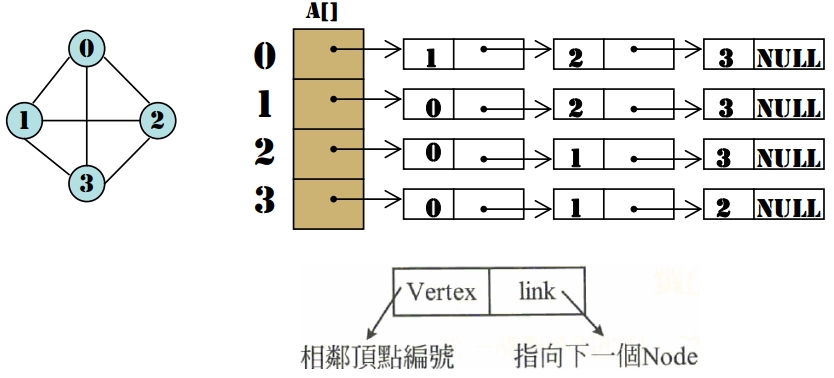

特質

  • 在無向圖中，相鄰串列的 Node 總數 = 2e ()

∵ 無向圖中，，∴ 在頂點為 i 的相鄰串列中會加入 的 Node；同時，在頂點為 j 的相鄰串列中會加入 的 Node - 每個 Node 所連接到的相鄰串列其長度等於該 Node 的分枝度

運作

  • 判斷邊 是否存在?
    • 做法： 檢査頂點為 i 的相鄰串列中，是否有 Node j 存在。(Yes: 存在, No: 不存在)
    • 時間複雜度： O(e) (∵ 與 相連的邊之個數有關，∴ 比相鄰矩陣花時間)
  • 求頂點 的分枝度?
    • 做法：求頂點 i 之相鄰串列的長度 (即：節點總數)
    • 時間複雜度： O(e)
  • 求圖形的邊數?
    • 做法： \[\begin{align} e &= \sum_{i=1}^n \frac{D_i}{2} \\ &= \sum_{i=1}^n \frac{\text{頂點 i 之相鄰串列長度}}{2} \\ &= \frac{\text{所有串列之節點總數}}{2} \end{align}\]
    • 時間複雜度： O(n + e)
  • 時間複雜度 O(n + e) 的進一歩分析:
    • 當圖形的邊很少的情況： 一個無向圖可以保持連通的最少邊數為 e = n-1。因此，O(n+e) = O(2n-1) ≒ O(n)
    • 當圖形的邊很多的情況：一個擁有最多邊數的圖形是完整圖 (Complete Graph)，即：。因此，
    • 由上述兩種情況分析，當圖形的邊很多的情況，使用相鄰串列來求圖形的邊數不見得比相鄰矩陣有利。然而，時間複雜度雖然可能會與相鄰矩陣相同，但是相鄰串列在資料結構上多存放了 link ，需要更多的記憶體空間來執行

有向圖

若 G = (V, E) 為一有向圖，|V| = n 且 |E| = e，則需使用 n 條相鄰串列與一個 Size 為 n 的一維矩陣 A[1, …, n]，其中A[i] 所存放的是頂點 i 的相鄰串列，此串列中毎個 Node 皆記録著與頂點 i 相鄰之其它頂點

範例:： (以Out-degree為主)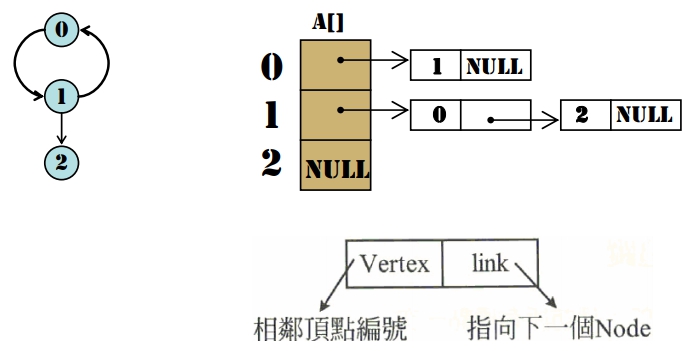

特質

在有向圖中，相鄰串列的 Node 總數 = e ∵ 有向圖中， 存在，不見得 也會存在

運作

  • 判斷邊 是否存在?
    • 做法： 檢査頂點為 i 的相鄰串列中，是否有 Node j 存在。(Yes: 存在, No: 不存在)
    • 時間複雜度： O(e) (∵ 與 相連的邊之個數有關)
  • 求頂點 的分枝度?
    • Out-degree：求頂點 i 之相鄰串列的長度 (即：節點總數；時間複雜度： O(e))
    • In-degree： 檢査所有串列，統計 Node i 出現的次數 (時間複雜度：O(n+e))
  • 求圖形的邊數?
    • 做法： \[\begin{align} e &= \sum_{i=1}^n D_i \\ &= \sum_{i=1}^n \text{頂點 i 之相鄰串列長度} \\ &= \text{所有串列之節點總數} \end{align}\]
    • 時間複雜度： O(n + e)

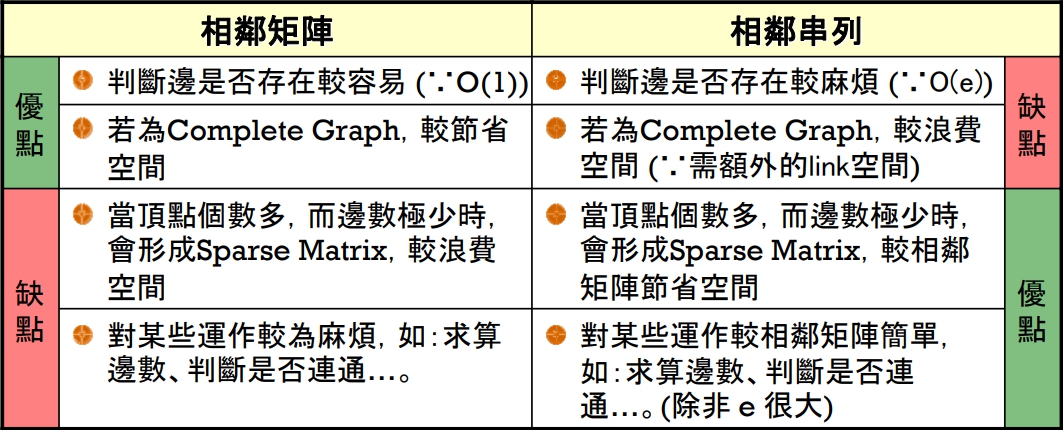
相鄰矩陣與相鄰串列的 比較

參考資料

國立聯合大學陳士杰資料結構