Insertion Sort

發表於 2020-12-30 Disqus：

文章字數： 1.6k 所需閱讀時間 ≈ 3 分鐘

想像手上有一副撲克牌，若想要將紙牌從左到右按照「小到大」排序。 Insertion Sort 的方法為：將第i張紙牌加入(insert)「前i−1張排序過」的紙牌組合，得到i張排序過的紙牌組合。給一張圖就很好理解: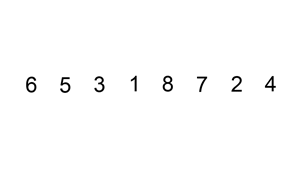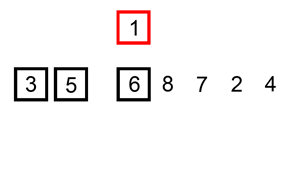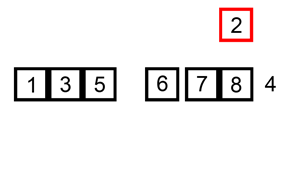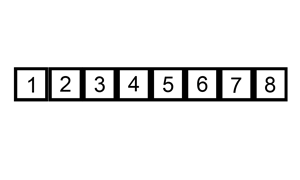

Algorithm 主要由 2 個副程式組成:

Insert

將某一筆記錄 x 插入到 S[1] ~ S[i-1] 等 i - 1 筆已排序好的串列中，使之成為 i 筆已排序好的串列
即: 決定 x 插入的位置

Sort

將未排序好的記錄透過 Insert 的動作，使之成為排序好的記錄
共需做 n - 1 回合，且由第二筆資料開始做起，∴ 迴圈: for i = 2 to n

程式碼

selection_sortview raw
def insertion_sort(collection: list) -> list:
    # 依序從collection[1:]開始往前插入
    for insert_index, insert_value in enumerate(collection[1:]):
        temp_index = insert_index
        # 檢查到index=0停止 and 一個一個往前比
        while insert_index >= 0 and insert_value < collection[insert_index]:
            # 往後移一個index
            collection[insert_index + 1] = collection[insert_index]
            # 繼續往前
            insert_index -= 1
        # 有改變index
        if insert_index != temp_index:
            # 前面while最後一行insert_index -= 1
            collection[insert_index + 1] = insert_value
    return collection


if __name__ == "__main__":
    from doctest import testmod

    testmod()

    user_input = input("Enter numbers separated by a comma:\n").strip()
    unsorted = [int(item) for item in user_input.split(",")]
    print(f"{insertion_sort(unsorted) = }")

特性

資料量少時較高效，且比其他的排序法高效（selection sort/bubble sort）。
自適應排序：可根據當前資料排序情形加速排序，資料越接近排序完成，效率越高。
穩定排序：相同鍵值的元素，排序後相對位置不改變。
原地排序：不需額外花費儲存空間來排序。
即時演算法：可處理逐步輸入的資料，不需等資料完全備妥。

變形

請參考 Binary Insertion Sort

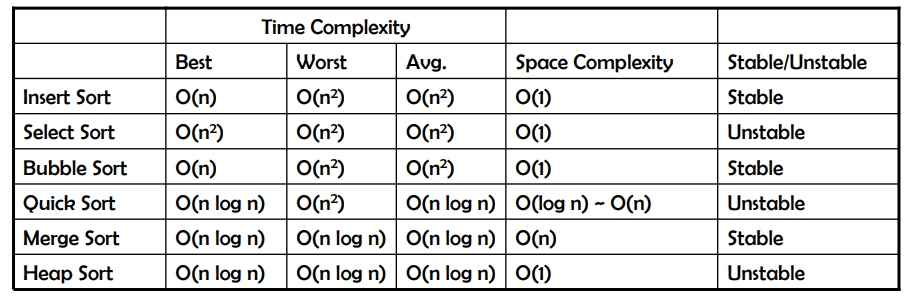
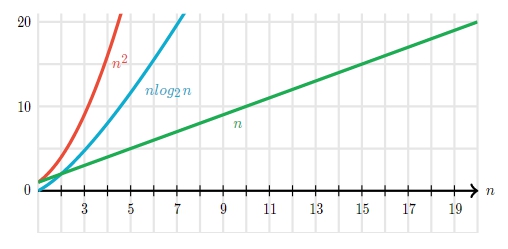
時間複雜度

best case

若要處理的 array 剛好是 ascending，那只要比較 n-1 次，所以 T(n) = T(n - 1) + 1

average case

T(n) = T(n - 1) + n/2

詳情請參考 Mordecai Golin：Average Case Analysis of Insertionsort

worst case

若要處理的 array 剛好是 descending，那麼第 i 個元素則需要向前比較 i-1 次，所以 n+(n-1)+...+1 = ，因此是 T(n) = T(n - 1) + (n - 1)

"Almost sorted" case

幾乎每次進到 insert 動作時( while 迴圈 )條件檢查就被擋下來，所以是 constant time，最外圈 loop( for迴圈 )執行 N-1 次。所以是。

空間複雜度

O(1)

Nicholas Blogger