Stack

發表於 2021-01-20 Disqus：

文章字數： 4.8k 所需閱讀時間 ≈ 9 分鐘

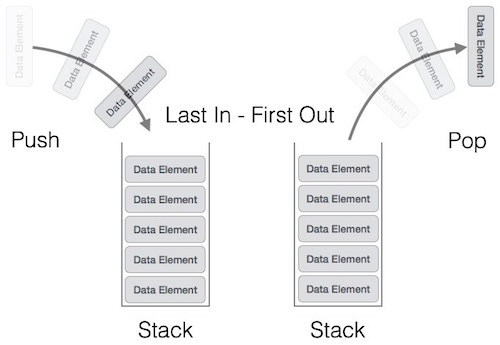
具有 LIFO (last in-first out) 或 FILO (first in-last out) 性質的有序串列

插入元素的動作稱為 Push, 刪除元素的動作稱為 Pop
Push/Pop 的動作皆發生在同一端，此端稱為 Top

Stack之ADT

ADT (Abstract Data Type; 抽象資料型態) - Def: ADT 是一種 Data Type，且要滿足：資料的規格與操作的規格獨立於資料的實際表示方式與操作的實際製作方式

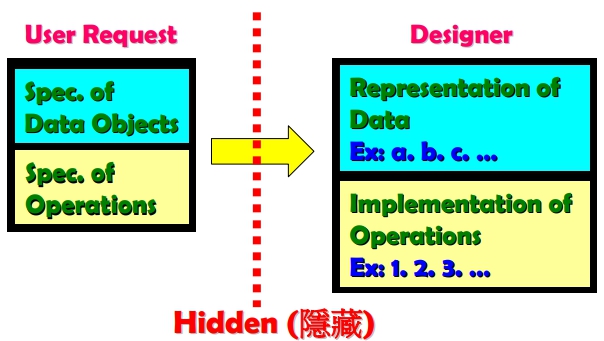
Data Object Spec

A set of data item
Top: 指出目前頂端元素所在
Size: 表Stack的大小

Operation Spec

Create(S) → S
Push(S, item) → S
Pop(S) → item, S
Top(S) → item
IsFull(S) → Boolean
IsEmpty(S) → Boolean

Stack 之製作

有兩個方式:

Array
Linked List

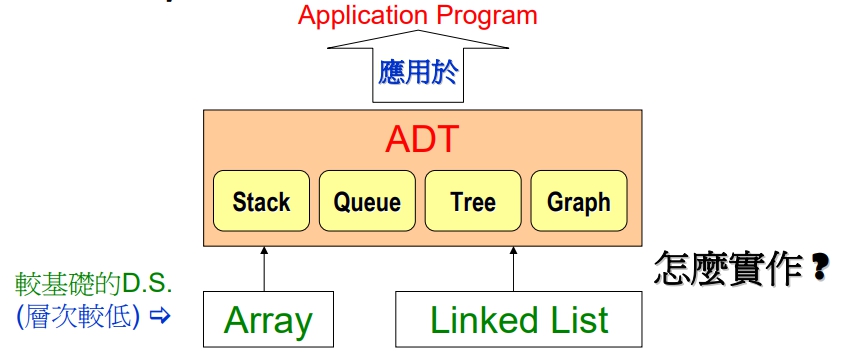
以 Array 製作 Stack

Create(S)

只需做宣告即可：

S: Array[1…n] item //宣告一個Array
int top = 0 //設定一整數變數top且初値為0

為了説明方便，這邊用 Array 製作 Stack 時，均假設一維陣列的起始位址是從 1 開始!

Push(S, item)

begin
  if top = n:
    stack Full;
  else:
    top = top + 1; //top要先加1
    S[top] = item; //再將item置入
end

Pop(S)

begin
  if top = 0:
    stack empty;
  else:
    item = S[top]; //先將item叫出
    top = top - 1; //再將top減1
end

Top(S)

begin
  if top = 0:
    stack empty;
  else:
    return S[top]; //將item叫出
end

IsEmpty(S)

begin
  if top = 0:
    return True;
  else:
    return False;
end

IsFull(S)

begin
  if top = n:
    return True;
  else:
    return False;
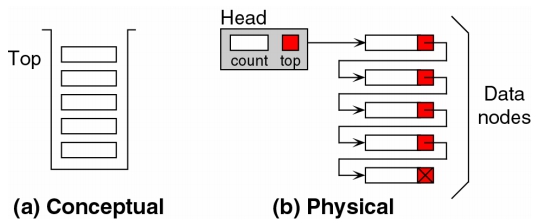
end

以 Linked List 製作 Stack

要利用 linked list 實作 stack，需要撰寫兩個不同的結構(Structure)：

Head：用以當作堆疊中的Top，以指出堆疊中頂端元素之所在
- 此 Head 結構內不一定要有存放資料之資料變數，但一定要有一個指標以指向堆疊的頂端元素
  往後文章若無特別説明，此 Head 結構皆僅有一個指標，名為“Top”
Data Node：用以存放欲置於堆疊中的資料
- 此節點的結構內至少要有一個指標與一個資料變數。指標用以指向下一個元素，資料變數用以存放堆疊的資料

Create(S)

宣告top指標為null即可:

top = null;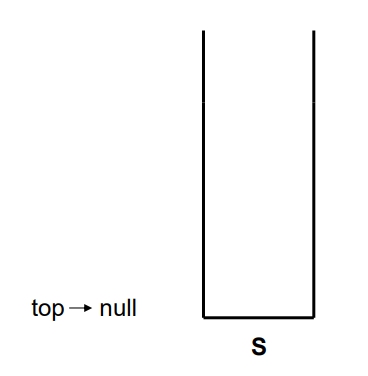

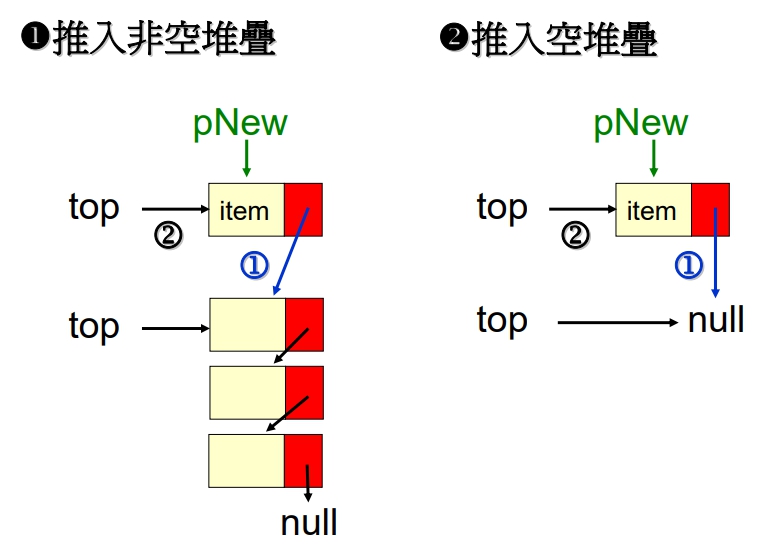
Push(S, item)

begin
  New(t); //跟系統要求記憶體空間以產生並置放一個新節點pNew
  pNew → data = item; //把資料 “item” 塞到這個新節點pNew的Data欄位中
1 pNew → link = top;
2 top = pNew;
end

只要 Memory 有空間，O.S.就允許 Linked Stack 去 Push 新資料!!不用像 Array 一樣，要先檢查 Array 是否滿了

Pop(S)

begin
  if (top = null):
    Stack empty;
  else:
1   dltPtr = top;
2   item = top → data;
3   top = dltPtr → link;
4   Ret(dltPtr);
end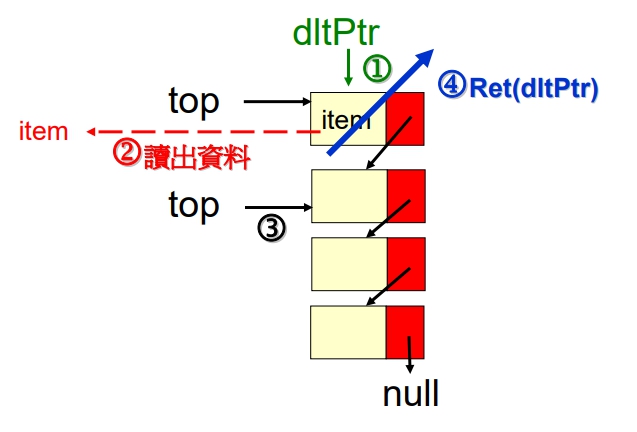

Top(S)

begin
if (top = null):
  success = false;
else:
  print(top → data);
  success = true;
return success;
end

IsEmpty(S)

begin
  if (top = null):
    result = true;
  else:
    result = false;
  return result;
end

IsFull(S)

begin
  if (memory available):
    result = false;
  else:
    result = true;
  return result;
end

Stack Application

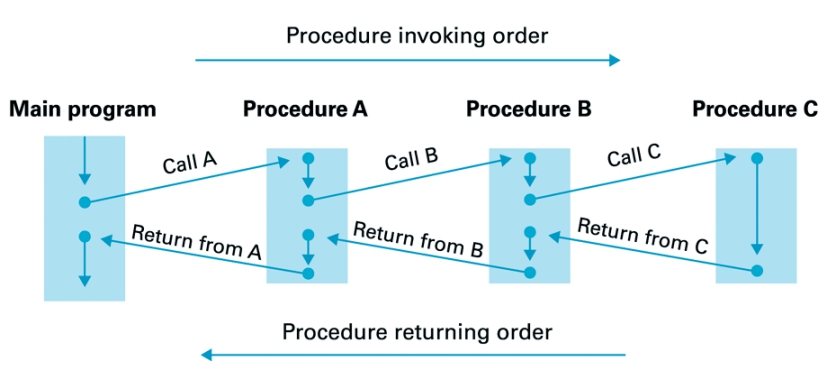
Procedure Call / Recursive Call 之處理

Parsing (剖析)

編譯器 (Compiler)將程式剖析成單獨的個體，如：關鍵字、名字、標誌…等，以進行程式語法檢査 - 一般常見的程式問題是不對稱的括號 (Unmatched Parenthese)，即是編譯器在剖析過程中，藉由堆疊來做判斷

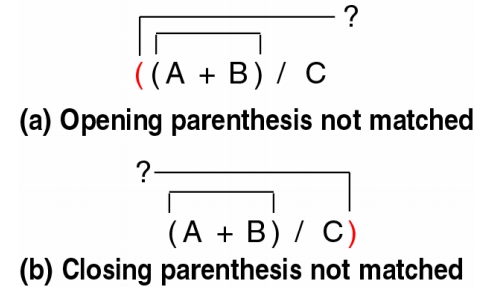
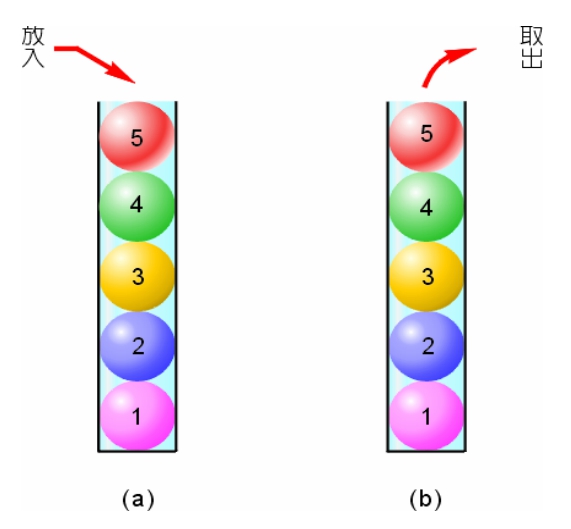
Reversing Data (反轉資料)

Infix 與 Prefix / Postfix 間互轉

Infix (中序式)

定義: 一般所使用的 Expression Format
形式: Operand 1 (運算元 1) Operator(運算子) Operand 2 (運算元 2)
運算子的種類:
- Binary: +, -, ÷, ×, and, or, …
- Unary: not
缺點: 不利於 Compiler 對式子運算的處理
- ∵需要考慮運算子之間的優先權、結合性
- ∴ Compiler 可能需要來回多次 scan 才可以求算出結果
- Ex: a + b * c ↑ (d - e)

Postfix (後序式)

形式: Operand 1 (運算元 1) Operand 2 (運算元 2) Operator(運算子)
優點:
- Compiler 易於處理，scan 一次即可求得計算結果
- ∵在後序式的表示式當中，已免除掉括號，優先權與結合性的考量
中序式轉後序式，需要用到一個 Stack 的支援

Prefix (前序式)

形式: Operator(運算子) Operand 1 (運算元 1) Operand 2 (運算元 2)
優點:
- Compiler 處理 Prefix 的計算，scan 一次即可求得結果
- ∵在前序式的表示式當中，已免除掉括號，優先權與結合性的考量
但是在中序式轉前序式比較麻煩，需要用到二個 Stack 的支援。∴還是傾向使用 Postfix

中序式與後序式 / 前序式互轉的計算

中序式轉後序式、前序式

使用 “括號法”:

中後的歩驟:
- 對於中序式，先加上完整的括號配對
- 將運算子取代最近的右括號
- 刪除左括號，予以輸出即可
中前的歩驟:
- 對於中序式，先加上完整的括號配對
- 將運算子取代最近的左括號
- 刪除右括號，予以輸出即可

一般常見的運算子之優先權與結合性: 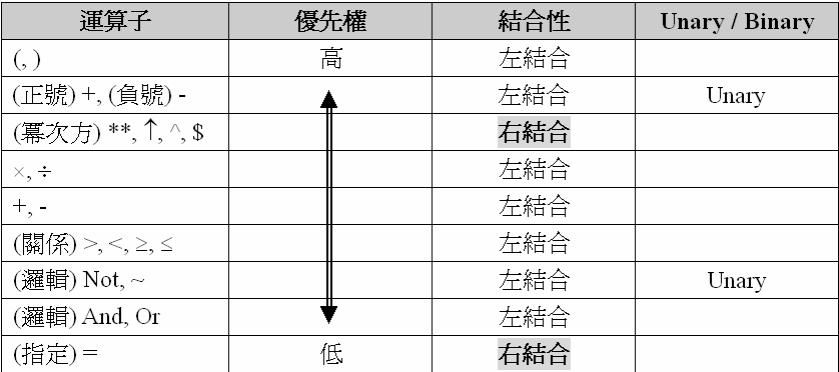以下是一些練習範例：

後序式、前序式轉中序式

很直觀，都是由左往右掃:

Prefix Infix
- Operator(運算子) Operand 1 (運算元 1) Operand 2 (運算元 2) Operand 1 (運算元 1) Operator(運算子) Operand 2 (運算元 2)
Postfix Infix
- Operand 1 (運算元 1) Operand 2 (運算元 2) Operator(運算子) Operand 1 (運算元 1) Operator(運算子) Operand 2 (運算元 2)

以下是一些練習範例：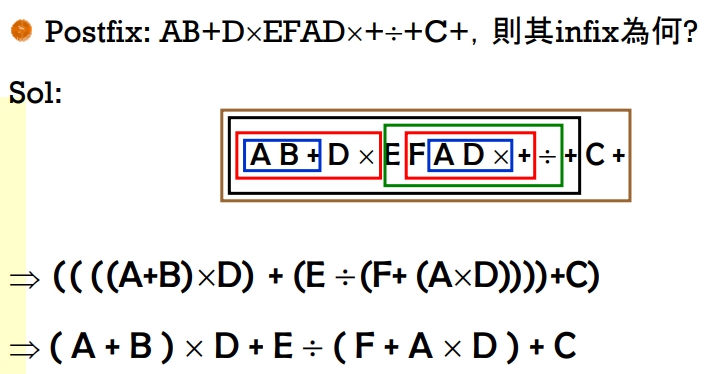

轉完中序後記得把多餘的括號拿掉

中序式與後序式 / 前序式互轉的演算法

需要堆疊(Stack)支援

Infix 轉 Postfix 的演算法 (利用1個Stack)

中序運算式由左往右掃描，當遇到:

運算元 : 直接輸出 (或Print) 到後序式
運算子 :
- ")": pop堆疊內的運算子直到遇到 "("
- 其它運算子x : 比大小
- 若運算子 x 的優先權 > 堆疊內最 Top 的運算子時，則將運算子 x push 至堆疊中
- 若運算子 x 的優先權 ≤ 堆疊內最 Top 的運算子時，則 pop 堆疊內的運算子直到 x > 堆疊內最 Top 的運算子為止

掃描完中序運算式，則將堆疊內的殘餘資料pop完

Stack 為空時，其優先權最低。(∵ Stack 沒有任何運算子可與待輸入的運算子做比較)
“(” 在 Stack 外優先權最高，但在 Stack 內優先權最低

Ex. 寫出 Infix: A+B×(C-D÷E)+F 轉 Postfix 的過程:

Print ‘A’
‘+’ > 空的 Stack push ‘+’
Print ‘B’
‘×’ > ‘+’(堆疊的top元素) push ‘×’
‘(’ > ‘×’ push ‘(’
Print ‘C’
‘-’ > ‘(’ (on stack) push ‘-’
Print ‘D’
‘÷’ > ‘-’ push ‘÷’
Print ‘E’
‘)’ pop stack until ‘(’
1. Pop ‘÷’, print
2. Pop ‘-’, print
3. Pop ‘(’, 不用print
‘+’ ≤ ‘×’ > pop ‘×’, print
‘+’ ≤ ‘+’ > pop ‘+’, print
‘+’ > 空的 Stack push ‘+’
Print ‘F’
Scan 完畢，清空Stack pop ‘+’

Ans: ABCDE÷-×+F+

while (Infix尚未Scan完畢):
  x = NextToken; //Token是指運算的單元，可能是運算元或是運算子
  if (x是operand):
    print(x);
  else:
    if (x是 ‘)’ ):
      pop(S), 直到遇見 ‘(’ 為止;
    else:
      比較 (x與stack top之優先權)
      - case “x > top”: 則 push(x, S);
      - case “x ≤ top”: 則 pop(S), 直到 x > top為止, 再push(x, S);
while (stack ≠empty):
  pop stack;

Postfix 之計算的演算法

由左往右掃

while (Postfix尚未Scan完畢):
  x = NextToken; //Token是指運算的單元，可能是運算元或是運算子
  if (x是operand):
    push(x);
  else:
    pop適當數目的運算元
    - 計算
    - 再將計算結果push回stack
pop stack; //即為結果

Ex. 43-15×+，寫出postfix計算過程 (含Stack內容):

Push ‘4’
Push ‘3’
‘-’: 1.pop ‘3’與 ‘4’ 2.計算 4-3 = 1, 再 push ‘1’
Push ‘1’
Push ‘5’
‘×’: 1.pop ‘5’與 ‘1’ 2.計算1 × 5 = 5, 再 push ‘5’
‘+’:
1. pop ‘5’與 ‘1’
2. 計算1 + 5 = 6, 再 push ‘6’
Scan完畢，pop stack 6

Infix 轉 Prefix 的演算法 (利用2個Stack)

Prefix 之計算的演算法

以上兩者因為繁瑣且較少實做所以省略

Stack 的排列組合問題 (Stack Permutation)

三個資料 a, b, c 依序 push 入 stack，而過程中可插入 pop 動作，則合法的排列組合有哪些?
- abc → push a, pop, push b, pop, push c, pop
- acb → push a, pop, push b, push c, pop, pop
- bac → push a, push b, pop, pop, push c, pop
- bca → push a, push b, pop, push c, pop, pop
- cab → 無法
- cba → push a, push b, push c, pop, pop, pop
n 個資料執行 stack permutation，其合法的排列組合個數為多少? \[ \frac{1}{n+1}\begin{pmatrix}2n\\n\\\end{pmatrix}\Longleftarrow \bf{Catalmnn Number} \]
Catalmnn Number可用於表示:
- n 個 nodes 所形成的不同二元樹個數
  - 後續文章討論
- n 個 “(” 與 “)” 所形成的合法配對個數
  - ( ) ( ( ) )
  - ( ( ) ( ) )
  - ...
- n 個矩陣之所有可能相乘方式 (同 “括號配對”的觀念)
  - ...
- n 輛火車進出鐵軌問題

參考資料

國立聯合大學陳士杰資料結構