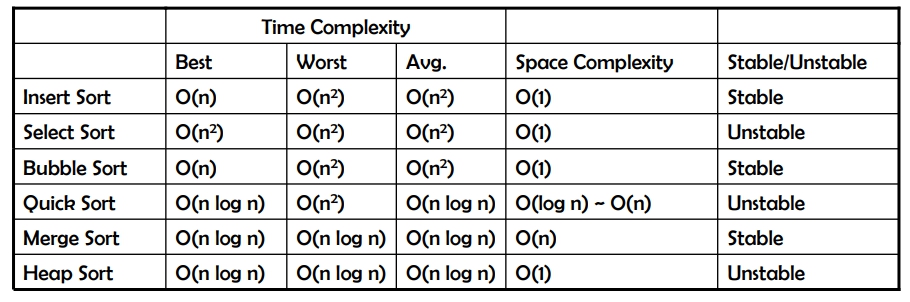
Quick Sort

快速排序 (Quick Sort) 的想法是說，先找一個基準點(pivot)，然後派兩個代理人分別從資料的兩邊開始往中間找，如果右邊找到一個值比基準點小，左邊找到一個值比基準點大，就讓他們互換。反覆找並互換，直到兩個人相遇。然後再將相遇的點跟基準點互換，第一輪結束。 接下來再分別從兩邊資料做子循環，但做法跟上面一樣，這就用到了遞迴的概念。

Algorithm

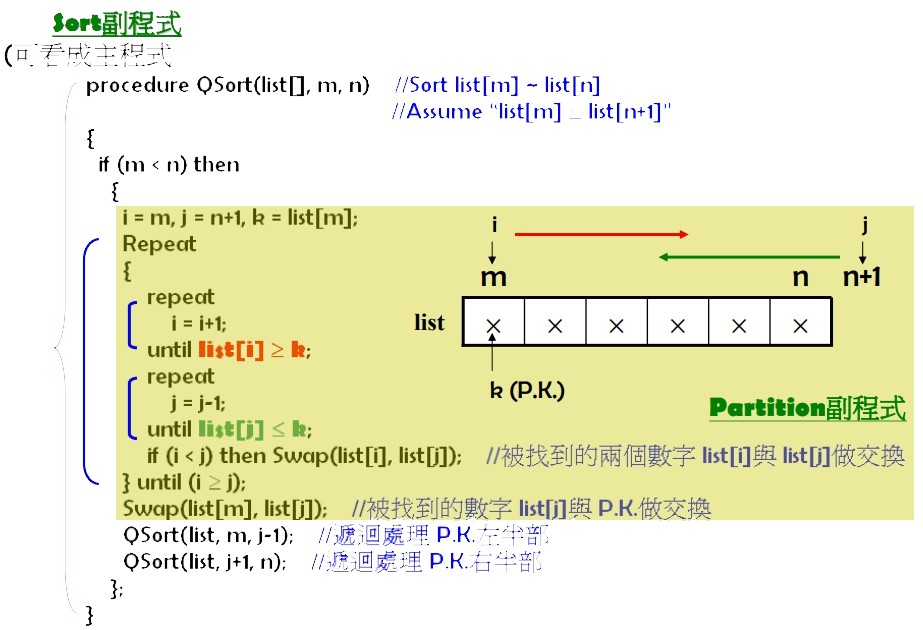
Algorithm 主要由 2 個副程式組成:

• Partition 副程式
  • 將記錄串中的第一筆記錄經過運算後，置於該記錄串中“最正確” 的位置上
  • 即: 找出 P.K.的最正確位置
• Sort 副程式(可當作主程式)
  • 將 Partition 後、位於 P.K. 前後未排序好的兩筆記錄串，透過遞迴的方式分別執行 Partition 副程式，使之成為排序好的記錄

---

假設我們現在有一筆班上的成績想要排序：

data = [89, 34, 23, 78, 67, 100, 66, 29, 79, 55, 78, 88, 92, 96, 96, 23]

1.先寫出遞迴函數架構

def quicksort(data, left, right):
    # 遞迴結束點
    if left >= right :
        return    
    # 左右指標指著
    i = left
    j = right
    # 基準點
    key = data[left]
    # 迴圈左右夾
    # code

2.由左(右)開始找出大(小)於基準點的值

while i != j:
    while data[j] > key and i < j:
        j -= 1
    # 注意 <=
    while data[i] <= key and i < j:
        i += 1
    # 如果兩者還未相遇
    if i < j:
        data[i], data[j] = data[i], data[j]

3.相遇點和基準點對調

data[left], data[i] = data[i], data[left]

4.左右遞迴下去

quicksort(data, left, i-1)
quicksort(data, i+1, right)

5.完整程式碼

方法一：

def quicksort(data, left, right): # 輸入資料，和從兩邊開始的位置
    if left >= right :            # 如果左邊大於右邊，就跳出function
        return

    i = left                      # 左邊的代理人
    j = right                     # 右邊的代理人
    key = data[left]                 # 基準點

    while i != j:                  
        while data[j] > key and i < j:   # 從右邊開始找，找比基準點小的值
            j -= 1
        while data[i] <= key and i < j:  # 從左邊開始找，找比基準點大的值
            i += 1
        if i < j:                        # 當左右代理人沒有相遇時，互換值
            data[i], data[j] = data[j], data[i] 

    # 將基準點歸換至代理人相遇點
    data[left] = data[i] 
    data[i] = key

    quicksort(data, left, i-1)   # 繼續處理較小部分的子循環
    quicksort(data, i+1, right)  # 繼續處理較大部分的子循環

quicksort(data, 0, len(data)-1)
print(data)

方法二： 詳細請參考Linear-time partitioning

# This function takes last element as pivot, places the pivot element at its correct position 
# in sorted array, and places all smaller (smaller than pivot) to left of pivot and 
# all greater elements to right of pivot 


def partition(arr, low, high): 
	i = (low-1)		 # index of smaller element 
	pivot = arr[high]	 # pivot 

	for j in range(low, high): 

		# If current element is smaller than or equal to pivot 
		if arr[j] <= pivot: 

			# increment index of smaller element 
			i = i+1
			arr[i], arr[j] = arr[j], arr[i] 

	arr[i+1], arr[high] = arr[high], arr[i+1] 
	return (i+1) 

# The main function that implements QuickSort 
# arr[] --> Array to be sorted, 
# low --> Starting index, 
# high --> Ending index 

# Function to do Quick sort 


def quickSort(arr, low, high):

	if len(arr) == 1: 
		return arr 
	if low < high: 

		# pi is partitioning index, arr[p] is now at right place 
		pi = partition(arr, low, high) 

		# Separately sort elements before partition and after partition 
		quickSort(arr, low, pi-1) 
		quickSort(arr, pi+1, high)

方法三： 利用 if..else 運算式語法，像 C/C++、Java 的 ?: 三元運算子功能

def quick_sort(collection: list) -> list:
    if len(collection) < 2:
        return collection
    pivot = collection.pop()  # Use the last element as the first pivot
    greater = []  # All elements greater than pivot
    lesser = []  # All elements less than or equal to pivot
    for element in collection:
        (greater if element > pivot else lesser).append(element)
    return quick_sort(lesser) + [pivot] + quick_sort(greater)


if __name__ == "__main__":
    user_input = input("Enter numbers separated by a comma:\n").strip()
    unsorted = [int(item) for item in user_input.split(",")]
    print(quick_sort(unsorted))

方法四：利用 for 包含式（Comprehension）

def quick_sort(data: list) -> list:

    if len(data) <= 1:
        return data
    else:
        return (
            quick_sort([e for e in data[1:] if e <= data[0]])
            + [data[0]]
            + quick_sort([e for e in data[1:] if e > data[0]])
        )


if __name__ == "__main__":
    import doctest

    doctest.testmod()

方法五:

random 選擇 index 當成 pivot，然後再和最左或最右的數交換後進行 normal quick sort。 random 選擇是為了改善 Quick Sort 在 Worst Case 下的執行時間: 避免挑到最小值或最大值作為 Pivot Key 類似的方法有 middle-of-three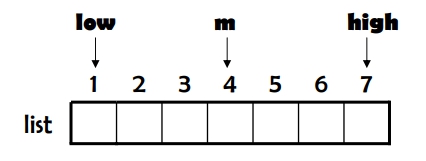

步驟: 1. m = [(low+high)/2] 2. 找出 list[low], list[m], list[high] 這三筆記錄的中間鍵值(即: 誰第二大) 3. 將此筆記錄與 list[low] 交換 4. 執行 Quick Sort

則可以可保証第一筆記錄絕對不是最小值或最大值

import random

def qsort(xs, fst, lst):
    '''
    Sort the range xs[fst, lst] in-place with vanilla QuickSort

    :param xs:  the list of numbers to sort
    :param fst: the first index from xs to begin sorting from,
                must be in the range [0, len(xs))
    :param lst: the last index from xs to stop sorting at
                must be in the range [fst, len(xs))
    :return:    nothing, the side effect is that xs[fst, lst] is sorted
    '''
    if fst >= lst:
        return

    i, j = fst, lst
    pivot = xs[random.randint(fst, lst)]

    while i <= j:
        while xs[i] < pivot:
            i += 1
        while xs[j] > pivot:
            j -= 1

        if i <= j:
            xs[i], xs[j] = xs[j], xs[i]
            i, j = i + 1, j - 1
    qsort(xs, fst, j)
    qsort(xs, i, lst)

與 Merge sort 差別

和 merge sort 一樣，quick sort 也是使用 divide-and-conquer。但是不一樣的是，merge sort 在 divide 階段幾乎沒做什事情，真正花時間的在 combine 階段。而 quick sort 則是相反，divide 花最多時間，而 combine 則沒做什事情。

時間複雜度分析

為什麼會有差異？

來自於基準點 pivot 的選擇 (partition)

Worst-case

當剛好每次 pivot 都選到該 array 最大或最小數時，如下圖。 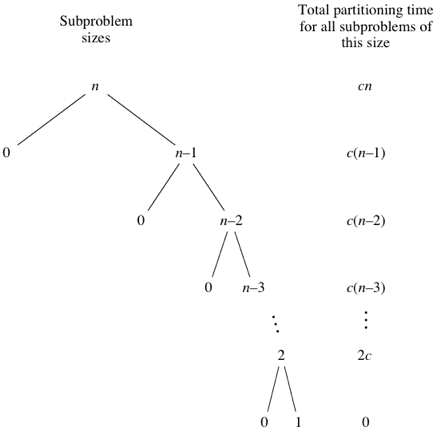加總起來後時間複雜度為 ，所以為

best case

最好的情況就是剛好把 subarray 分為一半(因 array 個數為奇數偶數而誤差 1 以內都沒差)，如下圖。 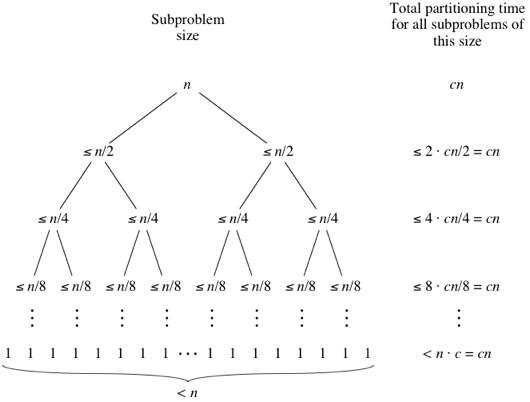和 merge sort 一樣，時間複雜度為:

average case

這裡直接說複雜度為:

因為推導需要複雜的數學運算，所以這裡只用簡單的例子說明(想像)一下。 假如每次分割剛好都分成 n/4 和 3n/4，則 tree 如下圖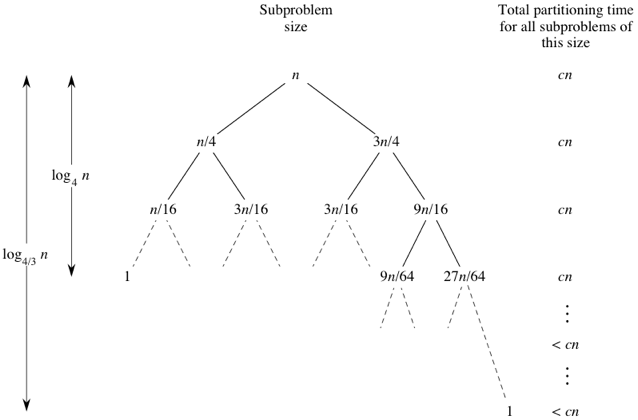： 先看 這層，共有 n 個節點。 這層以下的每層呢？都小於 n 個節點，所以花在 partition 的時間最多就 cn time 整體來看 tree 的右腳高度(最長)為 。現在已知數學式:對於所有的正數 a,b 和 n

\[log_an=\frac{log_bn}{log_ba}\]

所以最後時間複雜度也是為：

空間複雜度

• O(log n) ~ O(n)
  • 額外的空間需求，來自於遞迴呼叫所需的 Stack 空間
  • 而 Stack 空間的大小，取決於遞迴呼叫的深度
• Best Case: O(log n)
  • 由 Best Case 的時間複雜度分析可以得知，遞迴呼叫的深度是 log n，即: 做過 log n 次呼叫後，整體資料量只剩 1 筆，即可停止呼叫
• Worst Case: O(n)
  • 由 Worst Case 的時間複雜度分析可以得知，遞迴呼叫的深度是 (n - 1)，即: 做過 (n - 1) 次呼叫後，資料量只剩 1 筆，即可停止呼叫

Randomized quicksort

基本做法就是隨機選擇一數然後跟 left or right 對調，接著和原本的 quick sort 一樣。可參考上面方法五 可以延伸一些議題。(不過不重要，簡單的可以參考 Analysis of quicksort 最後一段)

參靠資料

• 快速排序法 (Quick Sort)
• Quick Sort
• Overview of quicksort
• Linear-time partitioning
• Analysis of quicksort
• 國立聯合大學陳士杰資料結構