Selection Sort

發表於 Disqus：
文章字數： 1.2k 所需閱讀時間 ≈ 2 分鐘

Selection Sort 的概念很簡單，假設有一個 array 需要排序，按照以下步驟排序。

  1. 找到最小的數，和第一個數 swap
  2. 找到第二小的數，和第二個數 swap
  3. 繼續往下找直到最後一個數

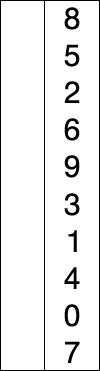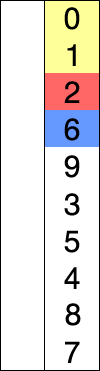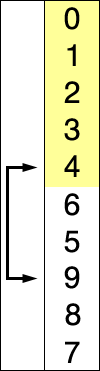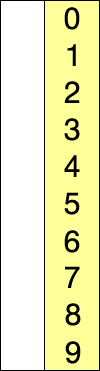
完整程式碼

selection_sortview raw
def selection_sort(collection):
    length = len(collection)
    for i in range(length - 1):
        least = i
        for k in range(i + 1, length):
            if collection[k] < collection[least]:
                least = k
        if least != i:
            collection[least], collection[i] = (collection[i], collection[least])
    return collection


if __name__ == "__main__":
    user_input = input("Enter numbers separated by a comma:\n").strip()
    unsorted = [int(item) for item in user_input.split(",")]
    print(selection_sort(unsorted))

特性

  • 對小資料序列排序效率較高
  • 不穩定排序：排序後，相同鍵值的元素相對位置可能改變
  • 原地排序：不需額外花費儲存空間來排序

不穩定排序

假定有一個序列要遞增排序，其中有重複的 2 元素，我們將其標上 2a、2b 以利辨識。 

[2a, 3, 4, 2b, 1]
開始迭代找出最小值並置換。 
 *             *
[1, 3, 4, 2b, 2a] # 1. 置換 2a, 1

     *     *
[1, 2b, 4, 3, 2a] # 2. 置換 3, 2b

        *       *
[1, 2b, 2a, 3, 4] # 3. 置換 4, 2a
有沒有發現， 2a 與 2b 的相對順序顛倒了呢？

問題出在 selection sort 是以置換的方式排序每次迭代的最小值。若我們將置換（swap）改為插入（insert），那麼 selection sort 就會是穩定排序，但相對地，需要位移剩餘未排序的元素，除非使用 linked list 或其他提供 insertion 的資料結構，不然就會多出額外 的寫入成本。

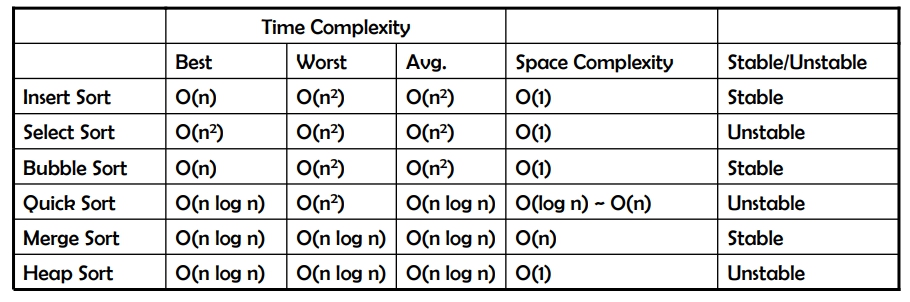
時間複雜度

Best / Average / Worst Case: \(O(n^2)\)

不論輸入資料如何，演算法中的兩個迴圈皆會執行

空間複雜度

O(1)

變形

Heapsort 是一個高效的排序法，使用 selection sort 融合 heap 這種半排序的資料結構，讓時間複雜度進化至 。更多詳情可以參考這篇介紹。

參考資料