Extended Binary Tree
具有 External Node 的 B.T. 稱之
- 一個二元樹具有 n 個節點,若以 Link List 表示,則會有
n+1 條空 Link,在這些空 Link 上加上特定節點,稱為 External Node (或 Failure Node),其餘 Nodes 稱Internal Nodes - 外部節點數 = 內部節點數 + 1 ( 2n – (n - 1) = n + 1 )
- 為何外部節點又被稱為失敗節點?
- 以
二元搜尋樹的角度來説,若搜尋到外部節點時,代表在原本的二元樹中找不到想要的資料,也就是搜尋失敗
- 以
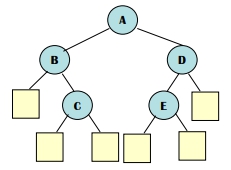
Internal path Length (I) and Extended path Length (E)
定義
\[ I = \sum_{i=1}^n Root 到內部節點 i 的路徑長度 \] \[ E = \sum_{i=1}^n Root 到外部節點 j 的路徑長度 \]
定理
E = I + 2n ( n 為內部節點個數 )
範例
- 範例 1: 一個具有 5 個 Internal Nodes 的 Extended B.T.,其 I 値與 E 値分別為?
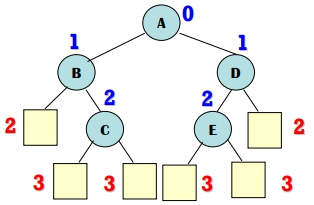
Ans:
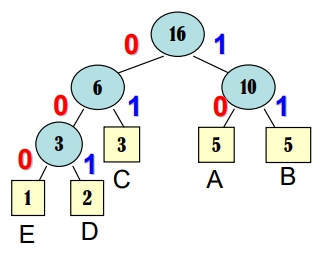
- I = 0 + 1 + 1 + 2 + 2 = 6
- E = 2 + 2 + 3 + 3 + 3 + 3 = 16 = I + 2n
- 範例 2: 一個具有 n 個 Internal Nodes 的 SkewedExtended B.T.,其 I 値與 E 値分別為?
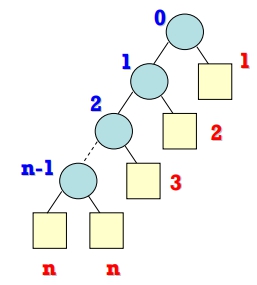
Ans:
- I = 0+1+2+…+(n-1) =
- E = 1+2+3+…+2n=
- I = 0+1+2+…+(n-1) =
結論
- E 値與 I 値成正比
- 愈平衡 (即:高度愈小) 的 Extended B.T.,其 E 値與 I 値愈小 (不考慮節點的加權值或加權值皆相同情況下)
- 然而,若
外部 Node 有加權値時,則第二個結論不見得成立
Weighted External Path Length (W.E.P.L.; 加權外部路徑長度)
定義
Extended B.T. 若有 n 個內部節點,則會有 n + 1 個外部節點。分別給予毎一個外部節點 1 個加權値,則: \[ W.E.P.L. = \sum_{j=1}^{n+1} (Root 到外部節點 j 的路徑長度) \times (外部節點 j 的加權值) \]
- 當節點有加權値,且毎個加權値不盡相同時,則當樹愈平衡時,不見得其外部路徑長度就愈小
問題:
- 若有三個 ( n 個 ) 內部節點,什麼情況它們的 Weighted E.P.L. 是最小的?
Min. W.E.P.L. ( 最小加權外部路徑長度 )
定義
給予 (n+1) 個外部節點加權値,在
應用
( n+1 ) 個訊息傳輸,其平均解碼時間最小 (或:編碼位元長度最小)
求 Min. W.E.P.L.的方法
- Brute Force 法 (暴力法)
Huffman Algorithm (霍夫曼演算法)
Huffman Algorithm (霍夫曼演算法)
令 W 為外部節點加權値的集合,Huffman Algo. 的執行歩驟如下:
- 自 W 中取出
2 個具最小加權値的節點 - 替這 2 個節點
建立 Extended B.T - 再將此 2 個節點的加權値和
加入 W中 - Repeat 前三歩直到 W 中只
剩一個加權値為止
範例
有 6 個外部節點,其加權値分別為: 2, 3, 5, 7, 9, 13。求 Min. W.E.P.L. 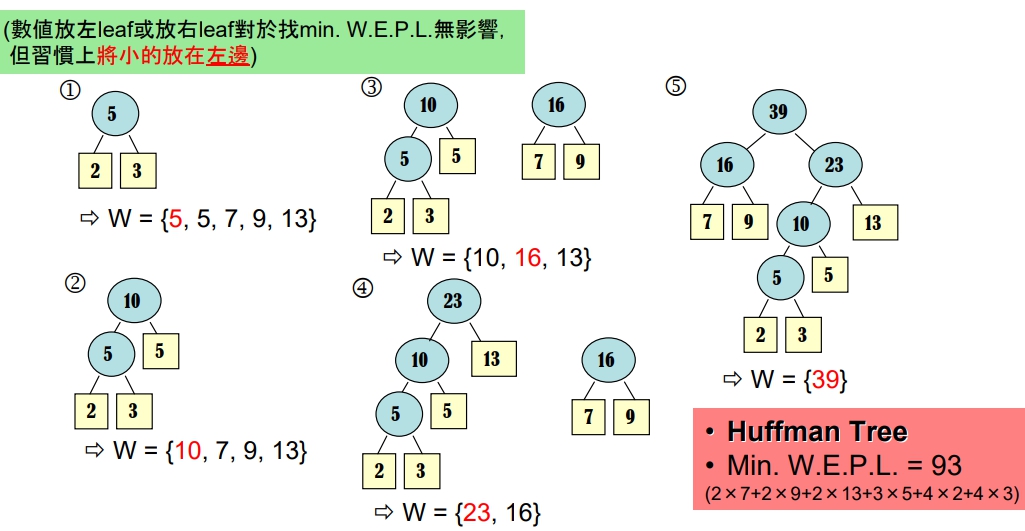
精神
- 若希望求得加權路徑長度總和為最小,則
加權値愈重的節點,離 Root 要愈近 - ∴ 建樹時是從底層建起;在建樹的過程中,皆是取
當時在 W 集合中權重値最輕的兩個節點
應用
- 有 6 個 Message 要傳輸,其出現頻率如下: \[ M_1 = \frac{2}{39}, M_2 = \frac{3}{39}, M_3 = \frac{5}{39}, M_4 = \frac{7}{39}, M_5 = \frac{9}{39}, M_6 = \frac{13}{39} \] 今希望平均解碼時間最小,則:
- 解碼時間最短的 Encoding / Decoding Tree 為何?
- 各 Message 之編碼內容為何?
- 平均最小編碼位元長度為何?
Ans:
Message:外部節點 出現頻率: 加權値
- 解碼時間最短的 Encoding / Decoding Tree :
- 將出現頻率通分後,以分子當加權値建立 Huffman Tree
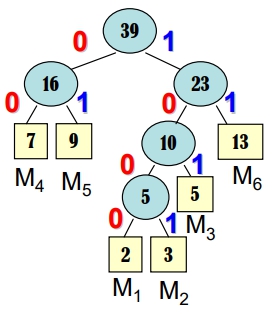
- Encoding / Decoding Tree (都是同一顆Tree):
- 左分支: 0
- 右分支: 1
- 將出現頻率通分後,以分子當加權値建立 Huffman Tree
- 各 Message 之編碼內容: (由 Root 開始走)
- Message Decoding Time = Message Bit 數 = Root 到外部節點的路徑長度
- 經常出現的訊息,Bit 數要愈少;即路徑長度要愈短
- 平均最小編碼位元長度:
- \[ \sum {(編碼位元數) \times (出現頻率)} \] \[ 2 \times \frac{7}{39} + 2 \times \frac{9}{39} + 2 \times \frac{13}{39} + 3 \times \frac{5}{39} + 4 \times \frac{3}{39} + 4 \times \frac{2}{39} = \frac{93}{39} \approx 2.38 \]
- 有一字串 AABBBACCBADDECBA,求 Encoding / Decoding Tree 為何?
Ans:
- 毎個字元的出現頻率:
- A: 5次
- B: 5次
- C: 3次
- D: 2次
- E: 1次