Queue

• 具有 FIFO (First-in, First-out) 性質的有序串列
• 插入與刪除元素的動作發生在佇列的不同端
  • 插入動作發生在尾端 (Rear)
  • 刪除動作發生在前端 (Front)

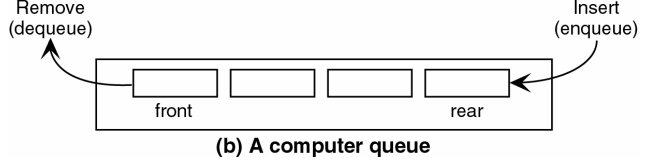
Queue 的應用

• 日常生活的排隊行為
• 在作業系統中的 job scheduling，在相同的 priority 下，利用 queue 來完成先到先做的策略
• 有許多的 I/O 工作同時要處理。將所有的 I/O 要求，利用 queue 來達成先到先做的策略
• 用於模擬 (Simulation) 方面，如佇列理論 (Queuing Theory)

Queue 的 ADT

Data Objects

• Queue: a set of data items
• Front: 指示Queue之前端元素所在
• Rear: 指示Queue之尾端元素所在

Operations

• Create(Q): 建立空佇列Q
• ADDQ(Q, item) → Q: 將 item 插入到 Queue Q 中，成為新的尾端元素(if Queue is full, then 無法執行)
• DeleteQ(Q, item) → item, Q: 刪除 Queue 中的前端元素 (if Queue is empty, then empty, then 無法執行)
• IsEmpty(Q) → Boolean
• IsFull(Q) → Boolean
• Front(Q) → item: 傳回 Queue 之 Front 端元素 (但不刪除)

Queue的製作

1. 用 Link list 製作
   • Single link list
2. 用Array製作
   • 利用 Linear Array
   • 利用 Circular Array with (n-1) space used
   • 利用 Circular Array with n space used

用 Linked list 製作

Create(Q)

宣告:

• rear: pointer = nil
• front: pointer = nil

ADDQ(Q, item)

• Case 1: (當Queue為空佇列)
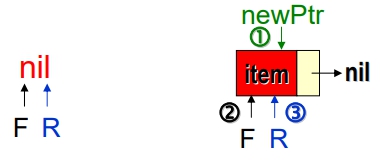
• Case 2: (當Queue不為空佇列)

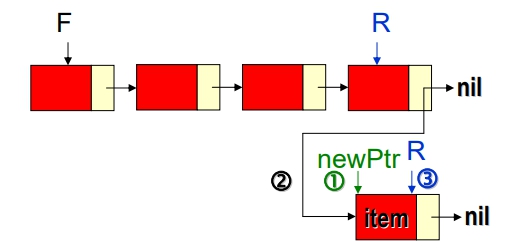
//F = front, R = rear
begin
  New(newPtr);
  newPtr → data = item;
  newPtr → link = nil; 
  if (rear = nil):         //Case 1
    front = newPtr;
  else:                    //Case 2
    rear → link = newPtr;
  rear = newPtr;
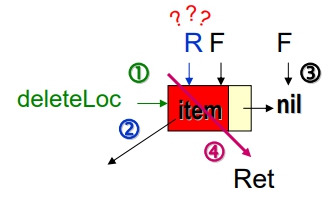
end

Delete(Q)

begin
  if (front = nil):
    Queue Empty;
  else:
1   deleteLoc = front;
2   item = front → data;
3   front = front → link;
4   Ret(deleteLoc);
    if (front = nil):   //見下面註釋
      rear = nil;
end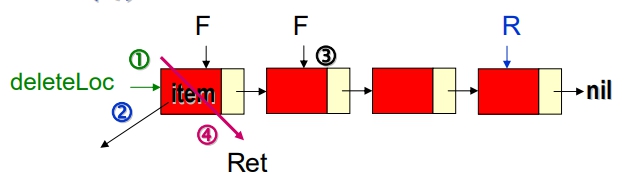

• 假設 Queue 中只有一個 node，回收後把 Rear 指向 nil
• 主要是擔心系統不會自動將 Rear 設成 nil，使得 Rear 指標無效

用 Array 製作

利用 Linear Array

Create(Q)

宣告:

• Q: array[0…n-1] of items //宣告 Q 是一個大小為n的一維 Array
• Front: integer = -1 //初値
• Rear: integer = -1 //初値

AddQ(Q, item) → Queue

begin
  if (rear = n):
    QueueFull;
  else:
    rear = rear +1
    Q[rear] = item
end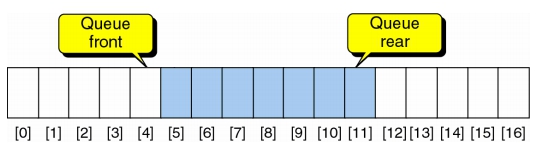

DeleteQ(Q) → item, Queue

begin
  if (rear = front):
    QueueEmpty;
  else:
    front = front +1
    item = Q[front]
end

問題: 當 rear = n 時，Queue 並不代表真正為滿的情況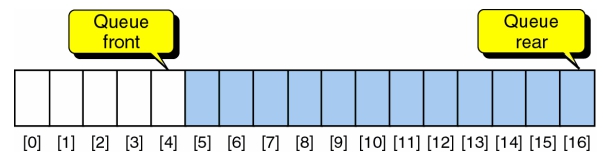

• 為解決上述問題，我們或許可以設計一個副程式，當資料已成長到 Arrar 的最末端時，作一次 “是否真的為滿” 的判斷 (即：Rear = n 且 Front = 0)。若不為真滿，則需將 (Front+1) 到 Rear 端的所有元素往左移 Front 格，並重設 Rear 與 Front 的指標値
• 然而，此種作法會導致 Queue 之 Add 動作時間為 O(n)
  • ∵是用廻圈來實作資料的搬移，花費時間太大。同時，此搬移工作是額外的處理項目，與 Add 動作本身是無關的
  • ∴當 Add 的工作很頻繁時，整體執行效益差

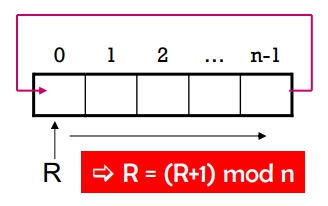
利用 Circular Array with (n-1) space used

Create(Q)

宣告:

• Q: Array[0…n-1]
• front = rear = 0 //初値

AddQ(Q, item) → Queue

begin
  rear = (rear+1) mod n ; //rear指標先前進
  if (rear = front):
    QueueFull;            //表示Queue滿了
    rear = rear-1 mod n;  //將rear重設回前一格
  else
    Q[rear]=item;
end

DeleteQ(Q) → item, Queue

begin
  if (front=rear): //先檢查
    QueueEmpty;
  else:
    front = (front+1) mod n;
    item = Q[front];
end

特點

• 最多只利用到 n-1 格空間
• 若硬要使用到 n 格空間，則 rear = front 條件成立時，無法真正區分出 Queue 為 Full 或 Empty
  • ∵ 判斷 Full 與 Empty 的條件式相同 (皆為 rear = Full)
• Add 與 Delete 之動作時間皆為O(1)
  • ∵ 沒有資料挪移的動作

利用 Circular Array with n space used

引進一個Tag 變數，用以協助判斷Queue 為 Empty 或 Full:

• 該變數為 Boolean 型態
• 若 Tag = True: 則可協助判斷是否為 Full
• 若 Tag = False: 則可協助判斷是否為 Null
• 不是光靠 Tag 就能做正確判斷

Create(Q)

宣告：

• Q: Array[0…n-1]
• front = rear: int = 0 //初値
• Tag: Boolean = 0 //初値

AddQ(Q, item) → Queue

begin
  if (rear = front and Tag = 1):
    QueueFull;
  else:
    rear = (rear+1) mod n; //rear指標前進
    Q[rear]=item;
    if (rear=front):
      Tag=1;
end

DeleteQ(Q) → item, Queue

begin
  if (Front=Rear and Tag=0):
    QueueEmpty;
  else:
    Front = (Front+1) mod n;
    item = Q[Front];
    if (Front=Rear):
      Tag=0;
end

特點

• 最多可利用到 n 格空間
• Add 與 Delete 之運作時間稍長
  • ∵多了一條 if 測試，來測試 Tag 値設定，且此兩個運作使用上極頻繁
  • ∴整體時間效益稍嫌 Poor

Queue的種類

FIFO Queue (先進先出佇列)

即一般的佇列，具有 FIFO 特性，前端刪除元素，尾端加入元素

Priority Queue (優先權佇列)

• 不一定遵守FIFO特性
• 運作：
  • 插入任意優先權値之元素
  • 刪除時，是刪除具最大/最小優先權値之元素
• 可利用 Heap (堆積) 來製作

Double Ended Queue (雙邊佇列)

• 可於任何一端執行插入/刪除元素的動作
• 亦可實作成：
  • Input-restricted：插入動作在固定端，刪除動作在任意端
  • Output-restricted：插入動作在任意端，刪除動作在固定端

Double Ended Priority Queue (雙邊優先佇列)

• 可於任何一端執行插入元素的動作。但刪除時，有一端是做 Delete Max 元素的動作，另一端則作 Delete Min 元素的動作
• 可利用 Min-Max Heap (堆積) 來製作

參考資料

國立聯合大學陳士杰資料結構