Graph
一個圖形(Graph) 是由頂點集合 V 與邊集合 E 所組成,表示如下: G (V, E) 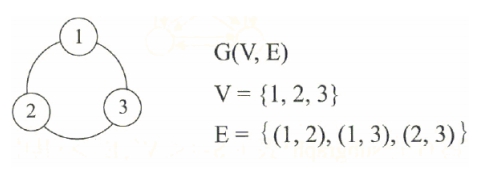
圖形種類
無向圖 (Undirected graph)
- G = (V, E), 其中 V 為頂點集合,E 為邊集合。 邊集合中的毎一個邊都
沒有方向性 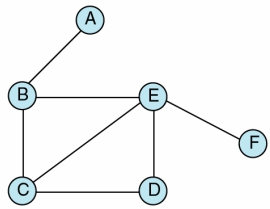
範例:
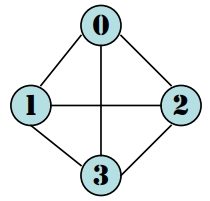
- V(G) = {0,1,2,3}
- E(G) = {(0,1), (0,2),(0,3),(1,2),(1,3),(2,3)}
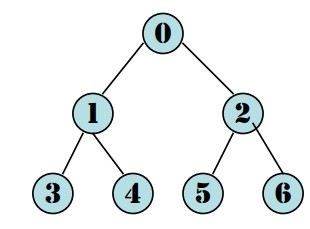
- V(G) = {0,1,2,3,4,5,6}
- E(G) = {(0,1), (0,2),(1,3),(1,4),(2,5),(2,6)}
有向圖 (Directed graph)
- G = (V, E), 其中 V 為頂點集合,E 為邊集合。邊集合中的毎一個邊都有
方向性,以指向下一個頂點 - 有向圖的邊有時亦稱為弧 (Arc)
範例:
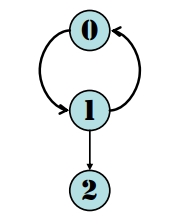
- V(G) = {0,1,2}
- E(G) = {(0,1), (1,0),(1,2)}
Terminology (相關術語)
Complete Graph (完整圖)
一個完整圖 (complete graph) 是一個擁有最多非重複邊線的圖
無向圖
若圖具有 n 個頂點,則具有最多的非重複邊個數達 n(n-1)/2 時,此圖稱為完整圖 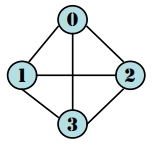
有向圖
若圖具有 n 個頂點,則具有最多的非重複邊個數達 n(n-1) 時,此圖稱為完整圖 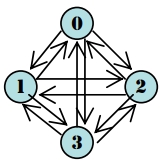 n(n-1) = 4(4-1) = 12 (非重複邊個數)
n(n-1) = 4(4-1) = 12 (非重複邊個數)
Subgraph (子圖)
若 G’ 是圖形 G 的子圖,則表示 V(G‘) ⊆ V(G) 且 E(G’) ⊆ E(G)
例:(以下子圖未完全列出) 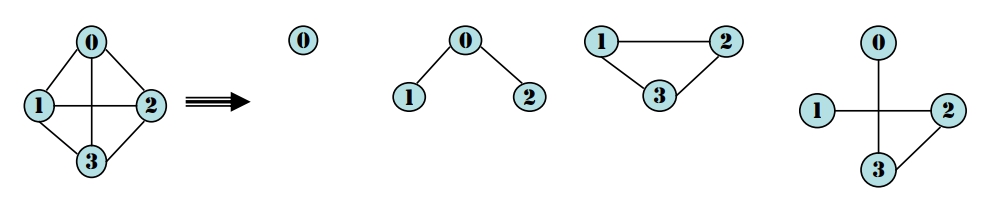
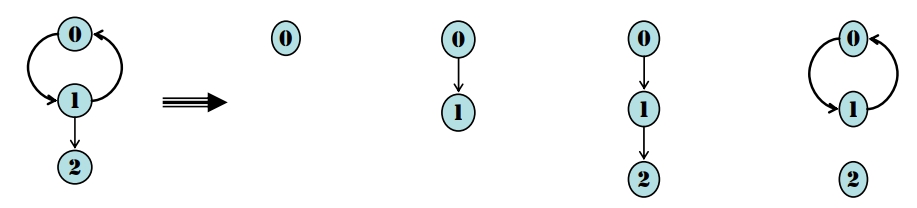
Path (路徑)
在圖形 G 中,由頂點
一連串頂點的集合一連串邊的集合
例: (以下路徑未完全列出)
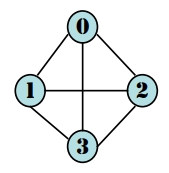
- 點
- 0 → 2 : (0, 1, 3, 2)
- 1 → 3 : (1, 2, 3)
- 0 → 1 : (0, 1, 3, 1)
- 邊
- 0 → 2 : (0, 1), (1, 3), (3, 2)
- 1 → 3 : (1, 2), (2, 3)
- 0 → 1 : (0, 1), (1, 3), (3, 1)
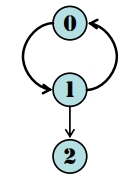
- 點
- 0 → 2 : (0, 1, 2)
- 1 → 2 : (1, 0, 1, 2)
- 邊
- 0 → 2 : (0, 1), (1, 2)
- 1 → 2 : (1, 0), (0, 1), (1, 2)
Path Length (路徑長度)
路徑上所包含的邊之數目
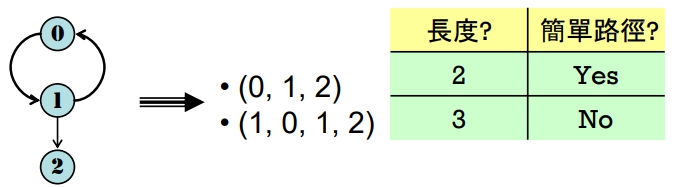
Simple Path (簡單路徑)
路徑上除了起點和終點可以相同之外,其餘頂點均不相同 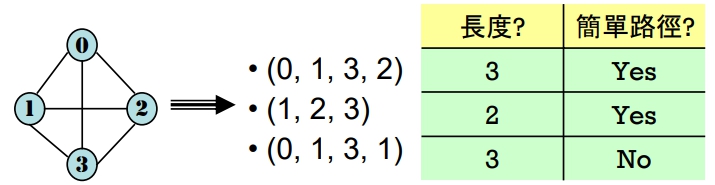
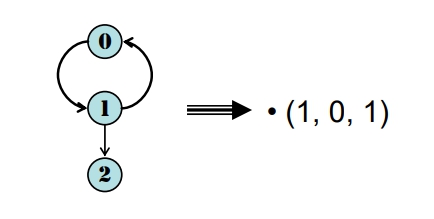
Cycle (迴圈)
是一個簡單路徑,且起點與終點相同 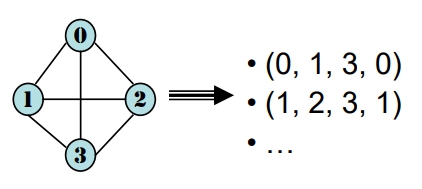
Connected (連通)
無向圖
在一 undirected graph 中,任何成對頂點之間皆有路徑存在 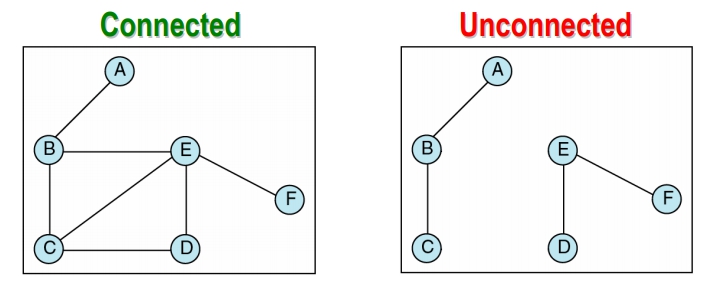
有向圖
- Strongly connected (強連通)
- 在有向圖形中,任何成對頂點之間
皆有路徑可以相互到達對方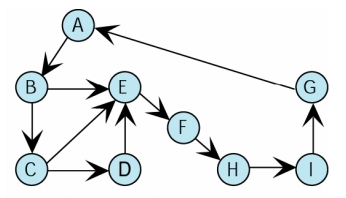
- 在有向圖形中,任何成對頂點之間
- Weakly connected (弱連通)
- 在有向圖中,至少有兩個頂點
無法以有向路徑相互到達對方 - 即:僅某一頂點可到達另一點,而另一點卻無法走回到對方
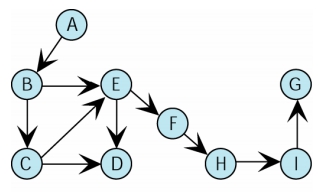
- 在有向圖中,至少有兩個頂點
- Disjoint (不相連)
- 一個有向圖形被切割成多個
互不相連的子圖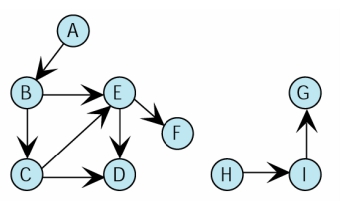
- 一個有向圖形被切割成多個
Degree (分枝度)
無向圖
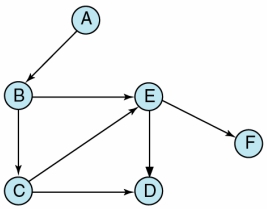
一個頂點的分枝度,為連接至該頂點的邊之個數 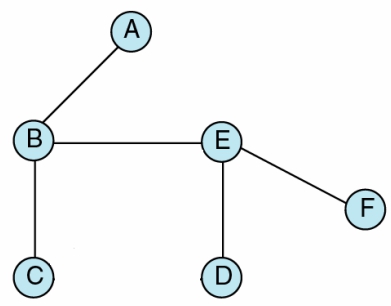 The degrees of the nodes A, C, D, F = 1
The degrees of the nodes A, C, D, F = 1
The degrees of the nodes B, E = 3
有向圖
一個頂點的分枝度,是由該頂點的入分枝度 (Indegree) 與出分枝度 (Outdegree) 加總而得
- Outdegree:一個頂點的出分枝度為
離開該頂點的邊之個數 - Indegree:一個頂點的入分枝度為
進入該頂點的邊之個數
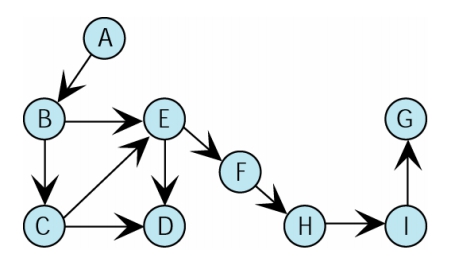
B 的 Indegree = 1; B 的 outdegree = 2; B 的 degree = 3
E 的 indegree = 2; E 的 outdegree = 2; E 的 degree = 4
Degree 與邊的關係
無向圖
\[\begin{equation}
\sum_{i=1}^n d_i = 2e \quad \therefore e = \frac{\sum d_i}{2} \quad (d_i : 指 V_i 的 degree)
\end{equation}\] 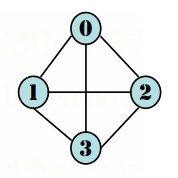
有向圖
\[\begin{equation}
e = \sum_{i=1}^n Indegree_i = \sum_{i=1}^n Outdegree_i
\end{equation}\] \[\begin{equation}
(Indegree_i : 指 V_i 的 indegree, Outdegree_i : 指 V_i 的 Outdegree)
\end{equation}\] 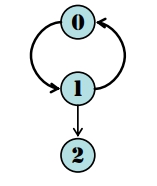 e = 3 (僅看 Indegree 或 Outdegree 的個數)
e = 3 (僅看 Indegree 或 Outdegree 的個數)