Merge sort
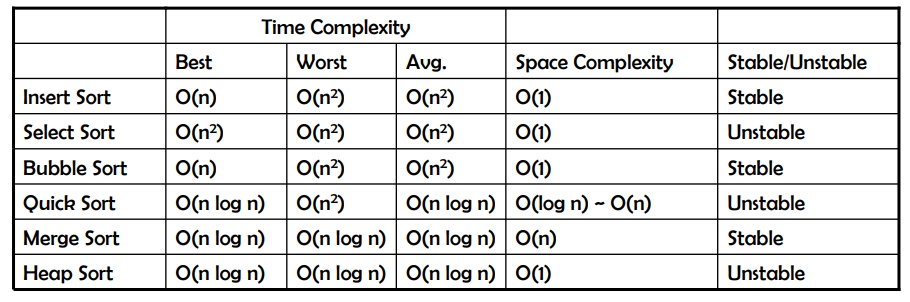
Merge sort 利用 divide and conquer 遵循以下三個步驟:
- Divide by finding the number q of the position midway between p and r. Do this step the same way we found the midpoint in binary search: add p and r, divide by 2, and round down.
- Conquer by recursively sorting the subarrays in each of the two subproblems created by the divide step. That is, recursively sort the subarray array[p..q] and recursively sort the subarray array[q+1..r]
- Combine by merging the two sorted subarrays back into the single sorted subarray array[p..r]
- base case: 一個 subarray 包含少於兩個數,即 p >= r,所以我們只在 p < r 時做 divide and conquer。
假設現在有一 array: [3, 7, 12, 14, 2, 6, 9, 11],下圖即是他的 divide and conquer 順序圖。
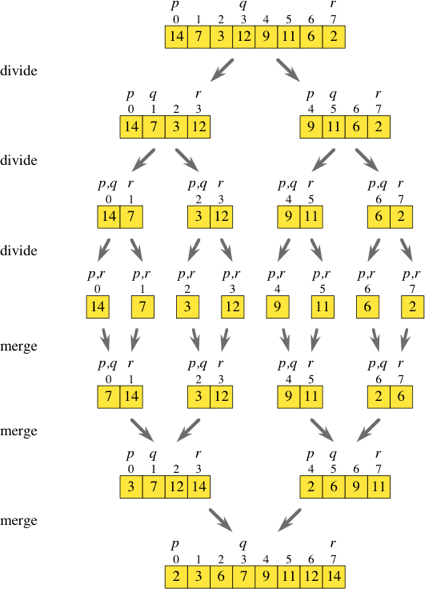
Merge
Merge sort 的關鍵在於 merge!
merge 時從兩個 array 的 index(0) 開始比較,比較小的數先進去 merge 後的 array,然後 index(1) 比 index(0) ...直到兩個 array 裡的元素都比完放入 merge 後的 array。 merge 總花費
time (可見 Linear-time merging 最後一段)
如下圖: 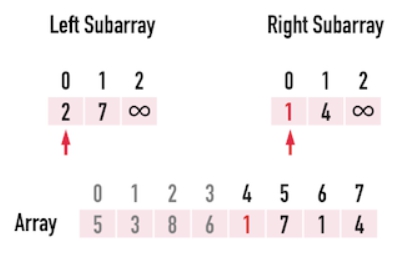 接著
接著 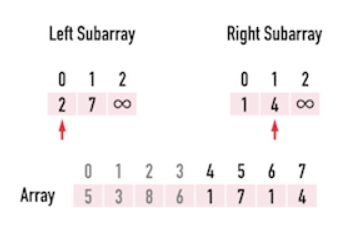 接著
接著 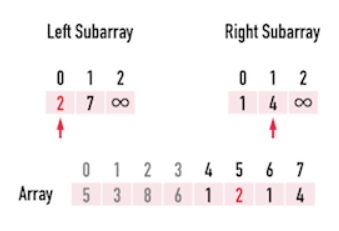
後記
有件事情值得注意,因為 merging 時,會複製出一個完整的 array(left_half_array, right_half_array),所以在同一時間所需的 space 非 constant,而 selection sort 和 insertion sort 在同一時間所需的 space 為 constant,所以此時可以按照 time 和 space 的衡量去使用適合的 sort algorithm。
程式碼
Recursive
Merge-sortview rawdef merge_sort(collection: list) -> list: def merge(left: list, right: list) -> list: def _merge(): while left and right: yield (left if left[0] <= right[0] else right).pop(0) yield from left yield from right return list(_merge()) if len(collection) <= 1: return collection mid = len(collection) // 2 return merge(merge_sort(collection[:mid]), merge_sort(collection[mid:])) if __name__ == "__main__": import doctest doctest.testmod() user_input = input("Enter numbers separated by a comma:\n").strip() unsorted = [int(item) for item in user_input.split(",")] print(*merge_sort(unsorted), sep=",")
Iterative
def merge(input_list: list, low: int, mid: int, high: int) -> list:
"""
sorting left-half and right-half individually then merging them into result
"""
result = []
left, right = input_list[low:mid], input_list[mid : high + 1]
while left and right:
result.append((left if left[0] <= right[0] else right).pop(0))
input_list[low : high + 1] = result + left + right
return input_list
# iteration over the unsorted list
def iter_merge_sort(input_list: list) -> list:
if len(input_list) <= 1:
return input_list
# iteration for two-way merging
p = 2
while p < len(input_list):
# getting low, high and middle value for merge-sort of single list
for i in range(0, len(input_list), p):
low = i
high = i + p - 1
mid = (low + high + 1) // 2
input_list = merge(input_list, low, mid, high)
# final merge of last two parts
if p * 2 >= len(input_list):
mid = i
input_list = merge(input_list, 0, mid, len(input_list) - 1)
p *= 2
return input_list
if __name__ == "__main__":
user_input = input("Enter numbers separated by a comma:\n").strip()
unsorted = [int(item.strip()) for item in user_input.split(",")]
print(iter_merge_sort(unsorted))時間複雜度
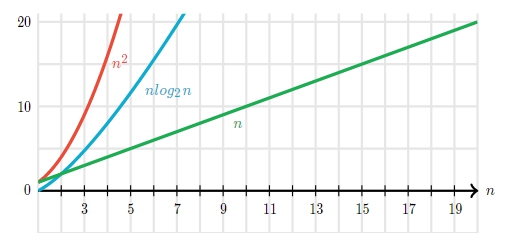
Avg. / Worst / Best Case: \(O(n\log n)\)
Recursive
時間函數: T(n) = T(n/2) + T(n/2) + c × n
- 最後合併左右兩半部所花時間
- ∵ 左、右半部排好之後,各只剩一個 Run,且兩半部各有 n/2 的資料量,其最後一次合併時的比較次數
最多為 n/2 + n/2 -1 次,即約n-1次 - ∴時間的表示可為
c × n 次(∵ 為線性時間))
- ∵ 左、右半部排好之後,各只剩一個 Run,且兩半部各有 n/2 的資料量,其最後一次合併時的比較次數
- 遞迴樹
- 步驟:
- 將原本問題照遞迴定義展開
- 計算每一層的 Cost
- 加總每一層的 Cost 即為所求
- 步驟:
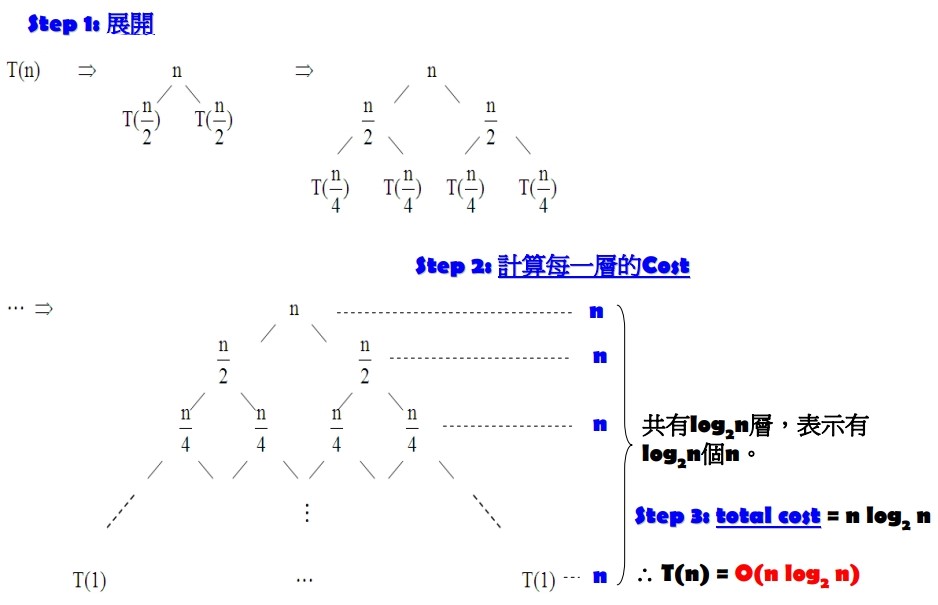
- 數學解法

∴ 總共花 O(n log n)
Iterative
排序 n 個資料,需花費 \(\lceil \log_2n \rceil\) 回合,且每一回合需花費 n + m - 1 = O(n) 時間做 Merge
- 不論哪一回合,merge 的時間都是與資料量呈線性變化
∴ 總共花 O(n log n)
空間複雜度
- 不論是遞迴或是非遞迴方式,都需要暫時性的陣列空間,目的是用來暫存每回合 Merge 後的 Run 之結果。
- ∴ O(n)
Stable
∵ 因為先前設計的演算法 <=,所以其相對位置沒有改變,亦即沒有不必要的 Swap 發生 ∴ Stable