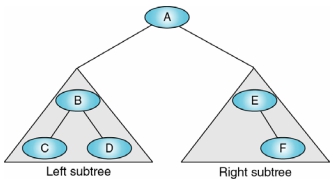
Binary Tree
- Binary Tree 為具有
≥ 0 個 nodes所構成的有限集合 - 表示各 node 之 degree 介於
0 與 2之間 - 左, 右子樹有
次序之分- 故又稱 Order Tree
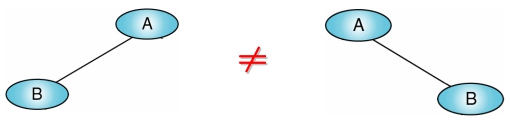
- 一般樹的子樹不會去區分是左子樹、中子樹還是右子樹,∵ 可能的子樹型態很多
- 故又稱 Order Tree
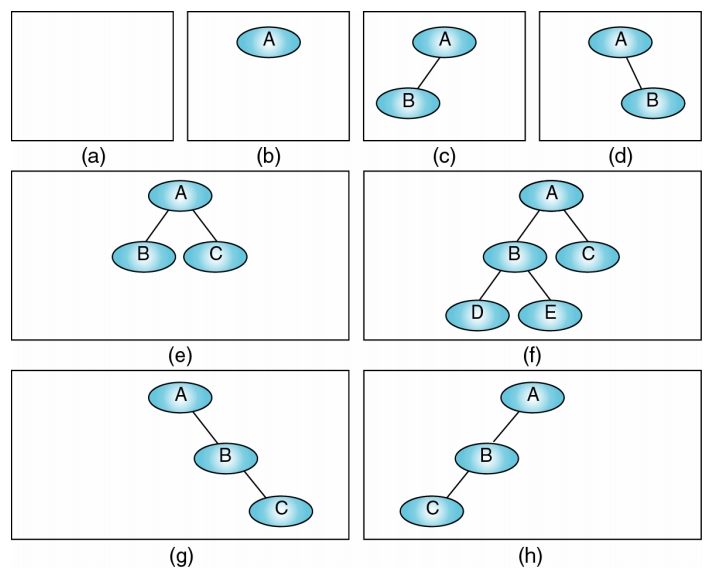
Tree 與 Binary Tree 之差異: 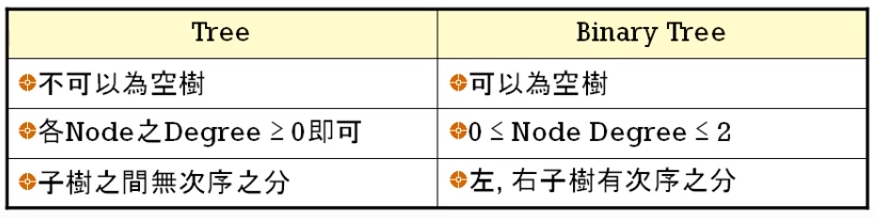
二元樹之三個基本定理
- 二元樹中,第 i 個 level 的 node 個數最多有
個 - 高 (深) 度為 H 的二元樹,其 node 個數最多有
個 ( ) - 非空二元樹若 leaf 個數為
個,degree 為 2 的 node 個數為 個,則
練習範例:
- 若有 15 個 leafs,則 degree 為 2 的 node 數 = ?
- 14 個
- 若有 10 個 degree 為 2 的 nodes,則 leaf 個數 = ?
- 11 個
- 若二元樹有 53 個 nodes,其中 degree 為 1 的 node 數有 22 個,則 leaf 個數 = ?
- n = 53 =
- n = 53 =
二元樹的種類
Skewed Binary Tree (偏斜二元樹)
- Left-Skewed Binary Tree: 毎個 non-leaf node 皆只有左子節點
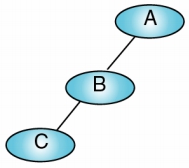
- Right-Skewed Binary Tree: 毎個 non-leaf node 皆只有右子節點
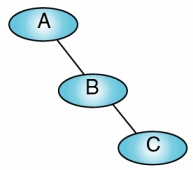
- 此類型的 tree 之高度 H 為節點個數 n
Full Binary Tree (完滿二元樹)
具有最多 Node 個數的二元樹稱之
- 即: 高度為 H,其 node 數必為
- Full B.T. 下具有 n 個 nodes,其高度必為:
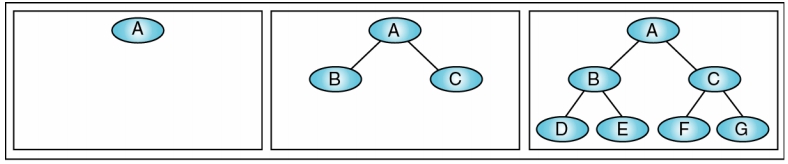
Complete Binary Tree (完整二元樹)
若二元樹高度為 H,node 個數為 n,則
- n 個 node 之編號與高度 H 的 full binary tree 之前的 n 個 node 編號一一對應,不能跳號
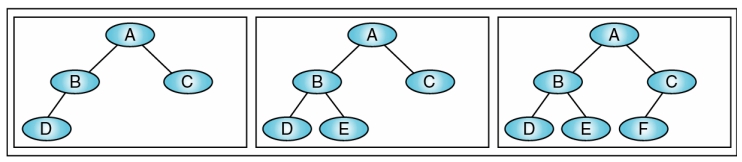
- Complete B.T. 下具有 n 個 nodes,其高度 H 必為:
- 假設 Complete B.T. 有 n 個節點 (編號 1~n),其中某個節點其編號為 i,則:
- 其左兒子編號為 2i; 若 2i > n,則左兒子不存在
- 其右兒子編號為 2i+1; 若 2i+1 > n,則右兒子不存在
- 其父點編號為 [
] ( [ ]: 無條件捨位取整數 ); 若 [ ] < 1,則父節點不存在
範例:
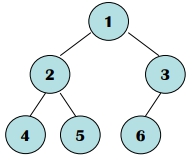
- 有一個 6 Nodes 的 Complete B.T.:
- Node 5 的 Parent 為何? 2
- Node 3 的 Sibling 為何?右子點為何? 2 , NULL
- Node 2 的左右子點和父點編號為何? 4, 5, 1
- Node 4 的 Grand Parent 為何? [
] 
範例:
- 有一個 Complete B.T.,共有 1000 個節點 (編號:1~1000)
- The number of “Last parent” = 500
- Node 256 的 Grand Parent = 64
- Node 347 的 Sibling = 346
- Node 450 的左子點 = 900, 右子點 = 901, 父點 = 225
- Node 600 的 左子點 = 不存在
- 樹高 =
= 10 - 有 500 個葉子節點
- Degree 為 1 的 Node 數有 1 個, 編號為 500
Binary Tree Structure
利用 Array
做法:
- 假設此二元樹的高度為 H,則準備一個大小為
的一維陣列 以相對於 Full B.T. 之節點編號,並將之一一對應填入
例:
此二元樹的高度為 3,則準備一個大小為 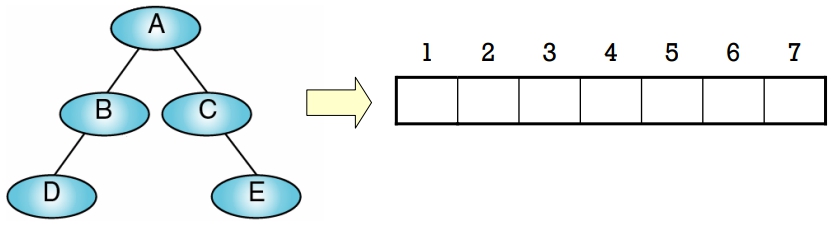
優點:
- 對於 Full B.T. 之儲存,完全沒有浪費空間
- 易於取得某 node 之左、右子節點及父節點之資料
- 當某個節點其編號為 i,則:
- 其左兒子編號為 2i,若 2i > n,則左兒子不存在
- 其右兒子編號為 2i+1,若 2i+1 > n,則右兒子不存在
- 其父點編號為 [
] ( [ ]: 無條件捨位取整數 ); 若 [ ] < 1,則父節點不存在
- 當某個節點其編號為 i,則:
缺點:
- 節點增刪不易
- ∵空間要費力移動。若空間不夠用時,需重新宣告 Array
對於 Skewed B.T. 之儲存,極度浪費空間
- 為何浪費空間?
- 假設有一個高度為 k 的
Skewed B.T.,則- 需準備一個具有
個空間之 Array - 實際會用到 k 個空間
- ∴ 會浪費
個空間
- 需準備一個具有
- 如: 有一個 k = 10 的 Skewed B.T.,需為它準備一個空間大小為 1023 的 Array,但實際卻只用上 10 個空間
- 假設有一個高度為 k 的
利用 Link List
節點結構設計如下: 
Node
leftSubTree <pointer to Node>
data <dataType>
rithtSubTree <pointer to Node>
End Node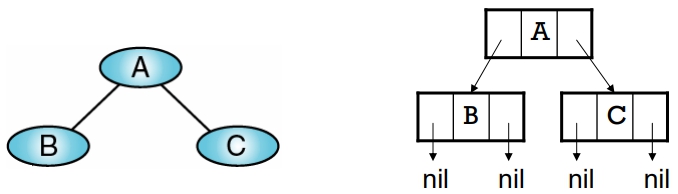
- 優點:
- 對於 Skewed B.T. 之儲存較 Array 節省空間
- Node 之增刪容易
- 缺點:
- 不易取得父點
- ∵ 指標只用以指向兩個孩子
- Link 空間仍浪費約一半
- 2n 個指標,n-1 個 node 頭上有指標
- 不易取得父點
- 分析: 假設 tree 有 n 個 nodes, tree degree 為 k
- 總共的 link 空間為: n
k - 有用的 link 空間 (即: link ≠ nil): n-1
- 浪費的 link 空間 (即: link = nil): nk - (n-1)
- 浪費比例:
- k 越
多,浪費比例越高- 若k=100,則浪費高達99%
- 為避免上述問題,則 k 應
越小越好。若:- k = 1
鏈結串列(∵ 不是 tree ∴ 不予討論) - k = 2
浪費比例最低
- k = 1
- k 越
- 總共的 link 空間為: n
Binary Tree Traversal (二元樹追蹤)
二元樹追蹤主要是拜訪二元樹中毎個 Node 資料各一次
Breadth-first Traversals (廣度優先追蹤)
由根節點出發,以水平方向由左到右處理,將所有同一 level 之節點拜訪完畢後,再選擇下一 level 之所有節點加以處理 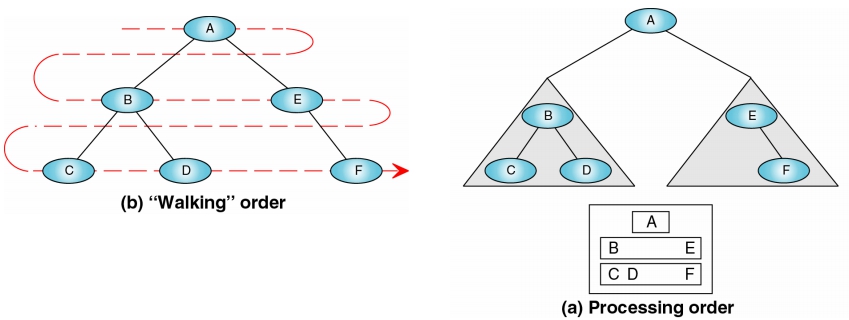
Depth-first Traversals (深度優先追蹤)
一個二元樹包括了根節點 (Root)、左子樹 (Left subtree) 與右子樹 (Right subtree),因此可能會有 6 種不同的 Depth-First Traversal 的走訪程序: 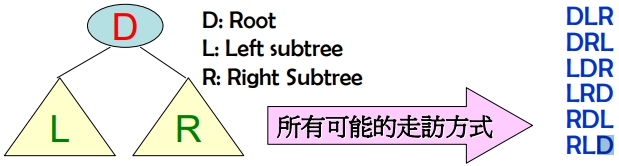
- 若限制 L 一定要在 R 之前走訪:
DLR: Preorder (前序)- L
DR: Inorder (中序) - LR
D: Postorder (後序)
- 看到 D 就印出 (處理) 資料 (
base case) - 上述走訪方式皆具備
遞迴特性
二元樹的追蹤次序與遞迴演算法
Preorder (DLR)
在前序追蹤時,根節點會最先被處理;再來是遞迴處理該根節點的左子樹;待左子樹之所有節點均處理完畢後,再遞迴處理該根節點之右子樹 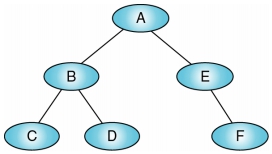 Output:
Output: ABCDEF
Procedure preOrder (T: Pointer to B.T. root)
if (T is not null): // 即: 樹為非空時
print (T → data); // D
preOrder (T → leftSubtree); // L
preOrder (T → rightSubtree); // R
return; // 由堆疊處取得應當返回之上層資訊
end preOrderInorder (LDR)
在中序追蹤時,需要最先遞迴處理根節點的左子樹;待左子樹之所有節點均處理完畢後,再處理根節點;最後再遞迴處理根節點之右子樹  Output:
Output: CBDAEF
Procedure inOrder (T: Pointer to B.T. root)
if (T is not null): // 即: 樹為非空時
inOrder (T → leftSubtree); // L
print (T → data); // D
inOrder (T → rightSubtree); // R
return; // 由堆疊處取得應當返回之上層資訊
end inOrderPostnorder (LRD)
在後序追蹤時,需要最先遞迴處理根節點的左子樹 ;待左子樹之所有節點均處理完畢後,再遞迴處理根節點之右子樹;最後再處理根節點  Output:
Output: CDBFEA
Procedure postOrder (T: Pointer to B.T. root)
if (T is not null): // 即: 樹為非空時
postOrder (T → leftSubtree); // L
postOrder (T → rightSubtree); // R
print (T → data); // D
return; // 由堆疊處取得應當返回之上層資訊
end postOrder配對問題
給予 “中序與前序”之配對,或是 “中序與後序”之配對,必可決定唯一的Binary Tree,但 “前序與後序”之配對無法決定出唯一的Binary Tree (可能會有很多組)
例1:
- 前序: ABCDEFGHI
- 中序: BCAEDGHFI
則此 Binary Tree 為何? (觀念: 用前序 DLR 決定 root ,用中序畫 tree) 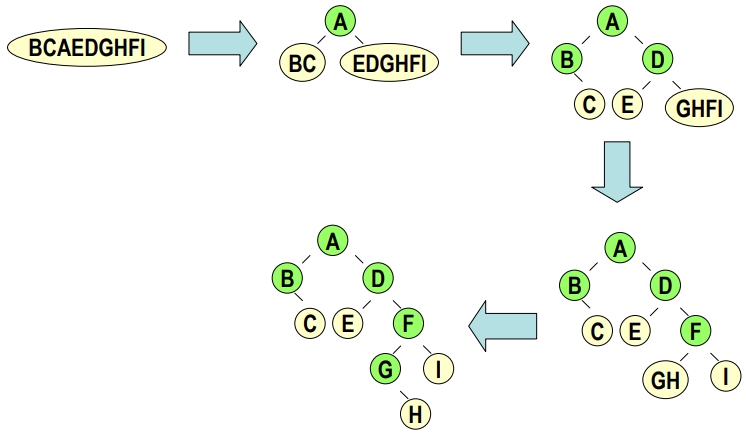
例2:
- 後序: EDBAJIHGFC
- 中序: ADEBCGHJIF
則此 Binary Tree 為何? (觀念: 用後序 LRD 決定 root ,用中序畫 tree) 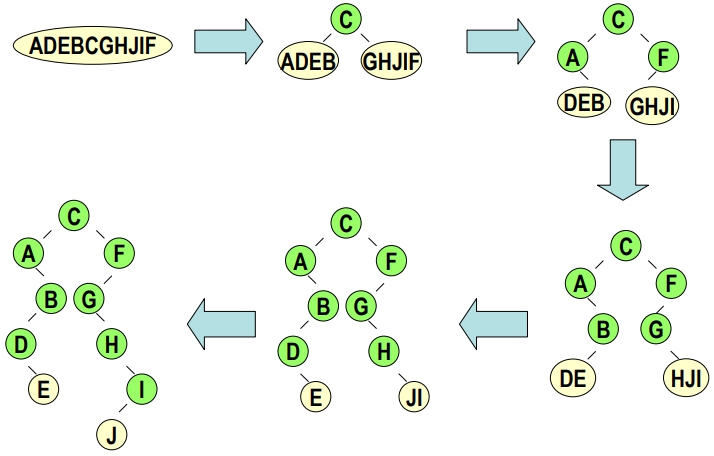
例3:
- 前序: ABC
- 後序: CBA
則此Binary Tree為何? 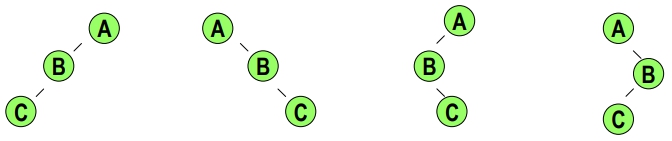
DFS 遞迴演算法其它應用
計算 B.T. 的節點總數
觀念:
- 若 B.T. 為空樹,則回傳結果為 0
- 若 B.T. 不為空樹,則:
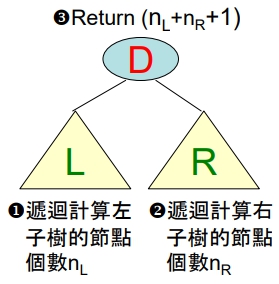
Procedure Count(T: Pointer of B.T. root)
if (T is not null): //即: 樹為非空時
nL = Count(T → leftSubtree);
nR = Count(T → rightSubtree);
return (nL + nR +1);
else:
return (0);
return;
end Count計算 B.T. 的高度
觀念:
- 若 B.T. 為空樹,則回傳結果為 0
- 若 B.T. 不為空樹,則:
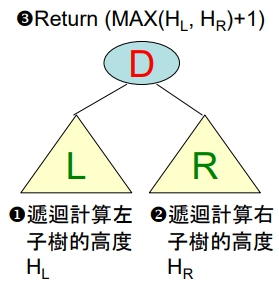
Procedure Height(T: Pointer of B.T. root)
if (T is not null): //即: 樹為非空時
HL = Height(T → leftSubtree);
HR = Height(T → rightSubtree);
return (HL + HR +1);
else:
return (0);
return;
end HeightB.T. 的毎一個節點之左右子樹互換
觀念:
- 若 B.T. 為空樹,則不需執行此工作
- 若 B.T. 不為空樹,則:
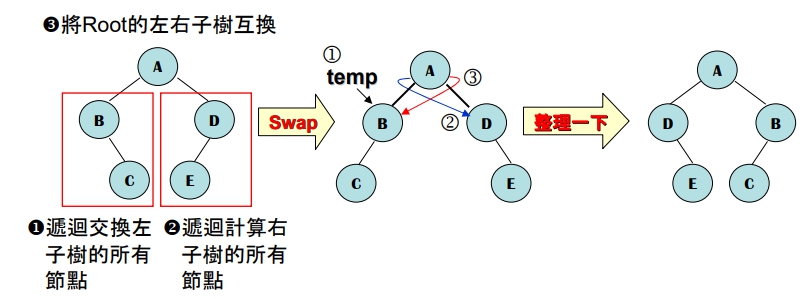
Procedure Swap(T: Pointer of B.T. root):
if (T is not null): //即: 樹為非空時
Swap(T → leftSubtree);
Swap(T → rightSubtree);
1 temp = (T → leftSubtree);
2 T → leftSubtree = T → rightSubtree;
3 T → rightSubtree = temp;
return;
end Swap二元搜尋樹
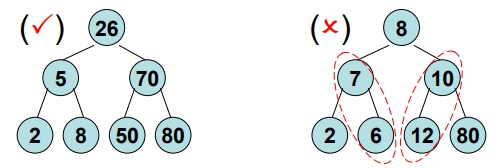
為一個 Binary Tree;可以為空,若不為空則需滿足:
- 左子樹所有 Node 鍵値均
小於Root 鍵値 - 右子樹所有 Node 鍵値均
大於Root 鍵値 - 左、右子樹亦是 Binary Search Tree
Binary Search Tree 可應用於資料的排序 (Sort) 與搜尋 (Search)
如何建立 B.S.T
- 依據資料輸入的順序,執行 “Insert a node into B.S.T”之工作:
- 輸入的資料皆與
樹根比,比樹根小就往左子樹放,比樹根大就往右子樹放
- 輸入的資料皆與
- 例:26, 5, 77, 43, 19, 2, 8
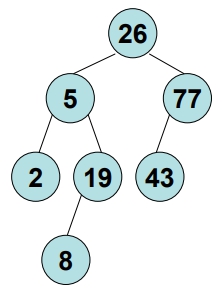
如何利用 Binary Search Tree 對資料進行排序 (Sort)
- 先將資料建成二元搜尋樹
- 依
Inorder追蹤,即可得出由小到大的排序結果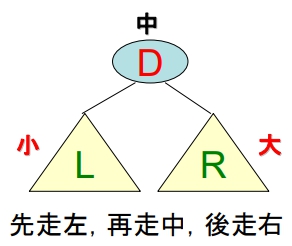
如何利用 Binary Search Tree 對資料進行搜尋 (Search)
- 演算法設計觀念:
- 如果在B.S.T.有找到想要的資料,則 return Data;否則就 return Not Found
- 假設要找的資料是 k,拿 k 跟樹根的資料 t 做比較:
- 若是 “
=”,表示找到資料 - 若是 “
<”,表示要往左子樹找 (遞迴) - 若是 “
>”,表示要往右子樹找 (遞迴)
- 若是 “
- 似 “前序追蹤” (DLR)
Procedure Search(T: Pointer to B.T. root, k: 要找的資料)
if (T is not null): //即: 樹為非空時
if (k = T → data):
return (T → data); // D
else if (k < T → data):
Search(T → leftSubtree); // L
else:
Search(T → rightSubtree); // R
else:
return “Not Found”;
return; //由堆疊處取得應當返回之上層資訊
end Search- 若有一個 7 個 Nodes 的 B.S.T. 如下,則其 “成功搜尋” 的平均比較次數為何?
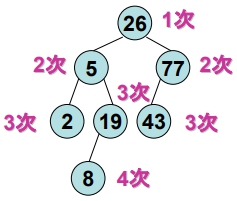 (1+2+2+3+3+3+4) / 7 = 18/7 (次)
(1+2+2+3+3+3+4) / 7 = 18/7 (次) - 若有一個 7 個 Nodes 的 B.S.T. 如下,則其 “成功搜尋” 的平均比較次數為何?
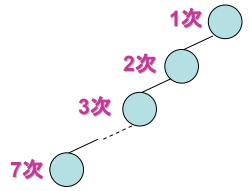 (1+2+3+4+5+6+7) / 7 = 4 (次) 此為 B.S.T. 從事資料搜尋的
(1+2+3+4+5+6+7) / 7 = 4 (次) 此為 B.S.T. 從事資料搜尋的最差情況 - 結論:
- 以 B.S.T. 從事資料搜尋時,其左、右子樹
愈平衡愈好 - B.S.T. 從事資料搜尋時,易受
資料輸入順序的影響
- 以 B.S.T. 從事資料搜尋時,其左、右子樹
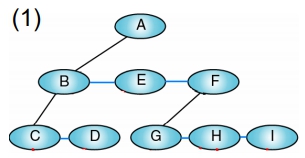
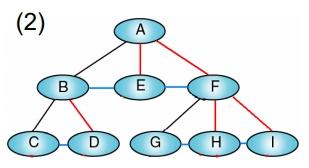
一般樹化成二元樹
做法:
- 建立 Sibling 之間的 Link
- 毎個節點只保留與原最左 (leftmost) child 間的 link 及 Sibling 間之 link,其餘父點與子點間的 link 皆刪除
- 順時針轉45度
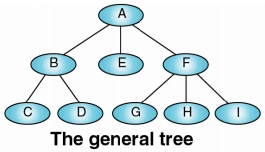
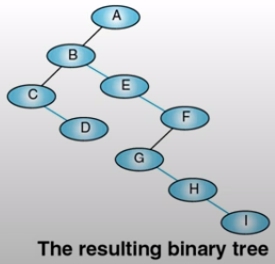
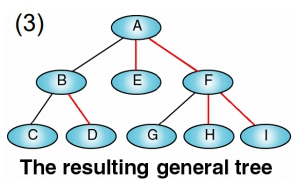
二元樹化成一般樹
做法:
- 逆時針轉 45 度 (即:右兒子上拉成右兄弟)
- 建立父點與子點之間的 links
- 刪除 Sibling 之間的 links
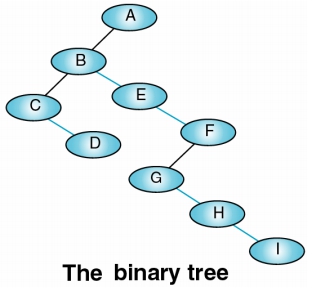
一般樹轉二元樹的陷阱
但是注意這邊的轉換: 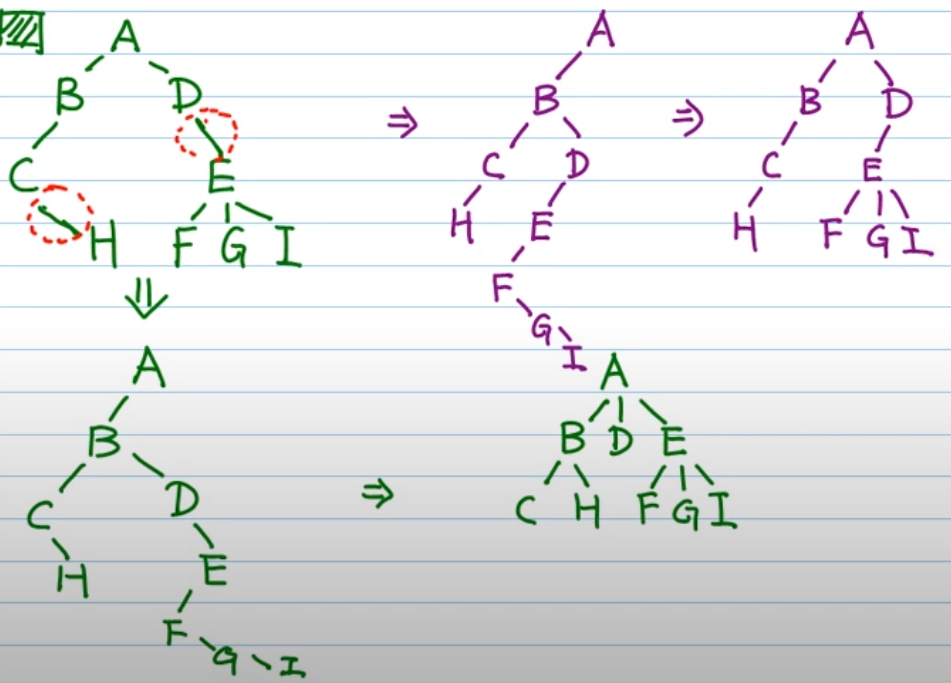
- 綠色轉換是
錯的(當 tree 的 node 只有右兒子時,轉成 binany tree 後還是右兒子,假如在轉回 tree 會發現長的不一樣了) - 紫色轉換才是
對的(假如 node 只有右兒子轉成 binany tree 時自動拉成左兒子,轉回 tree 後會發現一樣了)
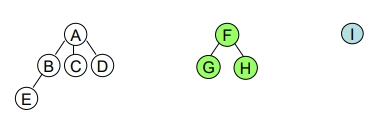
Forest 化成二元樹
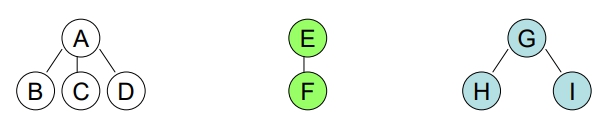
做法:
- 將森林中毎棵 Tree 先化成 Binary Tree

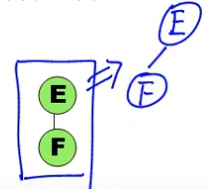
- 將各 Binary Tree 的 Root 以 Sibling 方式連結
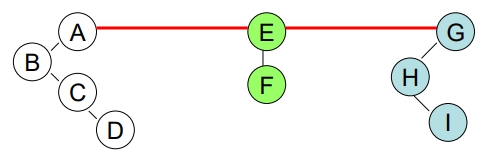
- 針對這些 Roots,順時針轉 45 度
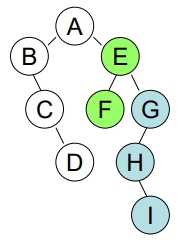
二元樹化成 Forest
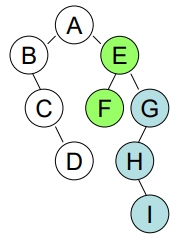
做法:
- 逆時針轉 45 度 (即:將 Root
右子樹中的所有最右節點上拉,以成為 Root 的右兄弟)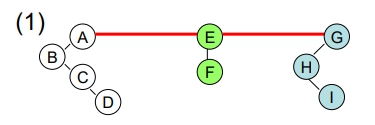
- 刪除 Root 間之 Sibling 的 links,以形成多個獨立的 B.T.
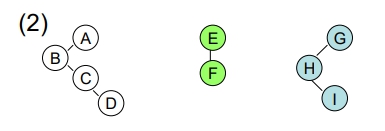
- 將各個 B.T. 化成一般樹
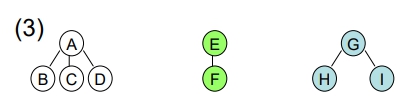
Forest 的追蹤
- Forest 之 Preorder、Inorder 等於 “
化成 B.T. 後,再利用 B.T. 的 Preorder、Inorder 追蹤” - Forest 之 Postorder
不等於“化成 B.T. 後,再利用 B.T. 的 Postorder 追蹤”
Preorder
先拜訪第一顆樹的 Root,再由左至右依序分別拜訪第一顆樹的子樹;接著再拜訪第二顆樹的 Root ,再由左至右依序分別拜訪第二顆樹的子樹;… (先處理某棵 Tree 的 Root,再處理子樹) 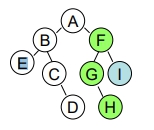
ABECDFGHI
Inorder
先由左至右依序分別拜訪第一顆樹的子樹,再拜訪第一顆樹的 Root ;接著再由左至右依序分別拜訪第二顆樹的子樹,再拜訪第二顆樹的 Root ;… (先處理某棵 Tree 的 子樹,再處理 Root) 
EBCDAGHFI
Postorder
先由左至右依序分別拜訪第一顆樹的子樹,接著再由左至右依序分別拜訪第二顆樹的子樹…。當拜訪完所有的子樹後,再由最後一顆樹的 Root 往回追蹤。 EDCBHGIFA
Thread Binary Tree (引線二元樹)
一個二元樹具有 n 個節點,以 link list 表示,會有 n+1 條空 links。為了充分利用這些空 links,將這些 links 改指向其它 nodes,此種 binary tree 稱為 Thread Binary Tree。一般而言,以中序引線二元樹居多。
- 若 x → Lchild 為 nil,則將 x → Lchild 改指向 x 在中序順序的
前一個 node - 若 x → Rchild 為 nil,則將 x → Rchild 改指向 x 在中序順序的
後一個 node
例:
給予一個二元樹如下,請繪出其 Thread B.T. 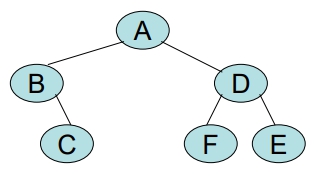
中序式: B C A F D E 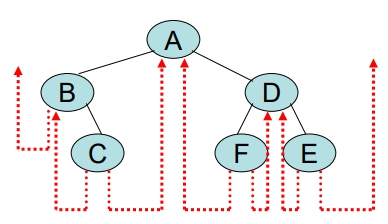
Data Structure 之設計

- Left Thread:
- True: 表 Lchild 為左引線指標
- False: 表 Lchild 為左兒子指標
- Right Thread:
- True: 表 Rchild 為右引線指標
- False: 表 Rchild 為右兒子指標
使用時,會再加入一個 Head Node (串列首)
- 空樹時:

- 非空樹時:
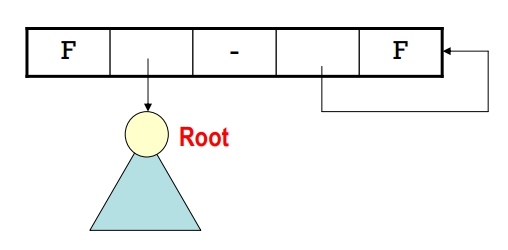
例:
將下列二元樹繪出其 Thread B.T. 之 Data Structure 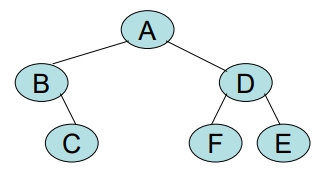
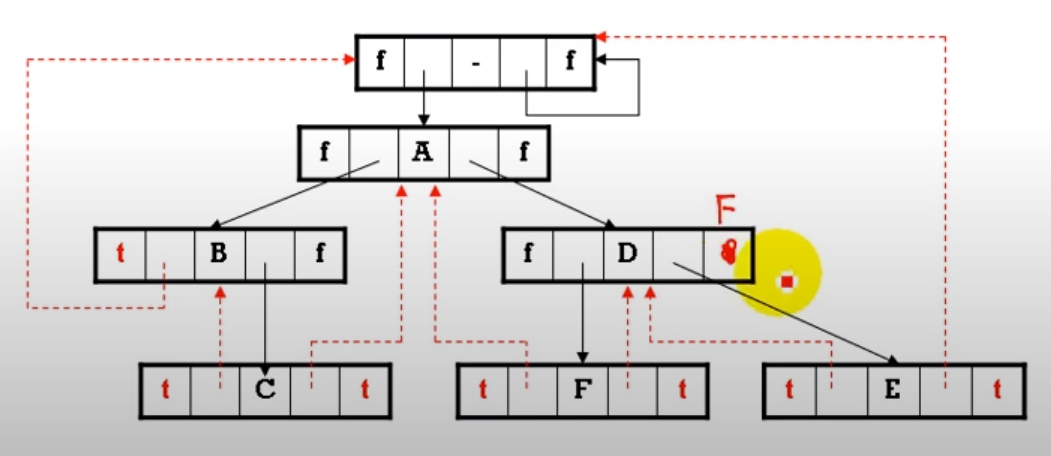
優點
- 充份利用空的 Link 空間
- 不需利用遞迴 (即:不需要 Stack 的支援),即可得到中序式,同時可立即知道某節點的中序後繼者與先行者
- 可簡化 Inorder traversal