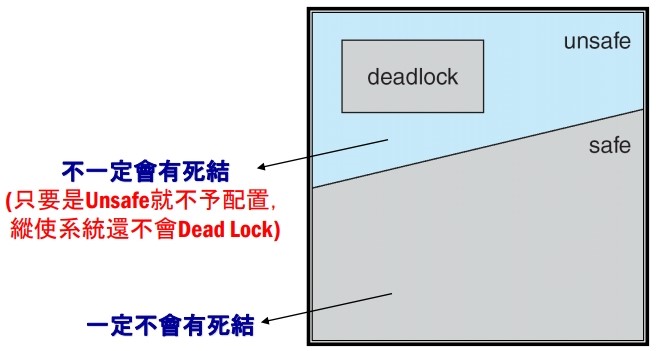
Dead Lock Avoidance

發表於 Disqus：
文章字數： 3.7k 所需閱讀時間 ≈ 7 分鐘

當 Process 提出對資源的申請時，O.S. 會根據以下資訊執行銀行家演算法 (Banker’s Algo., 內含 Safety Algo.)，來判斷系統在假設 核准申請後是否處於 Safe State。若是，則真的核准其請求；否則否決此次申請，Process 須再等待一段時間，下一次再提出申請。

  • 申請資源數量
  • 各 Process 目前所持有的資源數量
  • 各 Process 尚需要之資源需求量
  • 系統目前可用的資源數量

Banker’s Algorithm (銀行家演算法)

針對提出資源申請的 Process，來檢視系統 “是否會因接受此一 Process 的申請而進入死結。(內含 Safety Algorithm )

資料結構

Banker’s Algorithm 所使用的資料結構：(假設系統目前有 n 個 Process，與 m 種類型的資源)

  • \(Request_i[1…m]\)
    • 表示 Process i 所提出的資源申請量
    • 若 \(Request_i[j] = k\)，則表示 Process i 欲申請 k 個類型為 j 的資源
  • \(Allocation[1…n, 1…m]\)
    • 表示各 Process 目前持有的各類資源數量
    • 若 \(Allocation[i, j] = k\)，表示 Process i 目前持有類型為 j 的資源 共 k 個
  • \(Max[1…n, 1…m]\)
    • 表示各 Process 需要哪些資源、且需要多少數量才得以完成工作 (即： 記錄對各類資源的最大需求量)
    • 若 \(Max[i, j] = k\)，表示 Process i 需要有類型為 j 的資源，且最多要 k 個方可完成工作
  • \(Need[1…n, 1…m]\)
    • 表示 Process 目前尚需要多少數量的資源方得以完成工作
    • 若 \(Need[i, j] = k\)，則表示 Process i 尚需類型為 j的資源 k 個方能完成工作
    • \(Need_i = Max_i - Allocation_i\)
  • \(Available[1…m]\)
    • 系統目前各類資源的可用數量
    • Available = 系統資源總量 - Allocation

Algorithm

Banker’s Algorithm:

  1. 檢査 \(Request_i ≤ Need\)
  • 即：檢査所提出的需求合不合理
  • 不成立: 則 O.S.會視為 illegal，中止此 process
  • 若成立: 則 Go to 2
  1. 檢査 \(Request_i ≤ Available\)
  • 檢査系統是否有足夠資源可提供給 Process
  • 不成立: process 必須等待直到資源足夠
  • 若成立: 則 Go to 3
  1. (假設性試算)假設系統分配資源給該提出申請之 Process，透過計算下列數値以做接下來之安全演算法 (Safety Algorithm)之分析
  • \(Available = Available - Request_i\) (分配後的系統可用資源還有多少)
  • \(Need_i = Need_i - Request_i\) (分配後的 Process i 還需要多少資源才能完成工作)
  • \(Allocation_i = Allocation_i + Request_i\) (分配後的 Process i 所掌握的資源有多少)
  1. 執行 Safety Algorithm。
  • if 系統判斷會處於 Safe State，then 允許申請；
  • else 否決此次申請，稍後再重新申請

Safety Algorithm

Data Structures

Safety Algorithm 所使用的資料結構：(假設系統目前有 n 個 Process，與 m 種類型的資源)

  • \(Work[1…m]\)
    • 當假定配置資源後，目前系統可工作 (Work) 資源的數量累計
    • 初値 = Available
  • \(Finish[1…n]\) of Boolean
    • \(Finish[i]\) 表示 Process i 完成與否
      • True: 完成工作
      • False: 尚未完成
    • 初値: \(Finish[i]\) = False, i = 1 ~ n
      • ∵ Process 不可能一開始不取用任何資源就 Finish!

Algorithm

Safety Algorithm:

  1. 設定初値
  • Work = Available (分配後的系統可用資源還有多少。即：繼承前一個演算法的 Available 結果)
  • \(Finish[i]\) = False, i = 1 to n
  1. 找出一個 Process i，滿足：
  • \(Need_i\) ≤ Work

  • \(Finish[i]\) = False

  • 若找到，則 go to Step 3
  • 否則 go to Step 4
  1. 設定:
  • \(Finish[i]\) = True
  • \(Work = Work + Allocation_i\)，go to Step 2
  1. 檢査 Finish 陣列:
  • 若全部為 True，則系統處於 Safe State
  • 否則處於 Unsafe State

若可以找出至少一組 Process 執行順序，讓所有 Process 完成，此順序稱 Safe Sequence。(表示資源的分配、釋放 OK)

範例

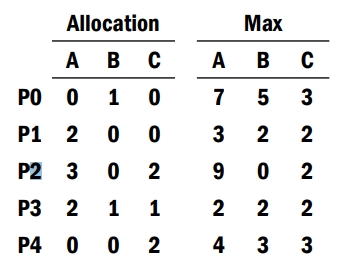
假設系統內有 5 個 Processes ( \(P_0\) ~ \(P_4\))及 3 種資源 A, B, C，其中 A 有 10 個，B 有 5 個，C 有 7 個。若系統目前状態如下表所示。則：

  1. Need 及 Available 的內容為何?
  2. 若\(P_1\)提出\(Request_1[1, 0, 2]\)，則系統是否核准?
  3. 若 \(P_4\) 再提出 \([3, 3, 0]\) 之請求，則是否核准?
  4. 若 \(P_0\) 提出 \([0, 2, 0]\) 之請求，則是否核准?

ANS:

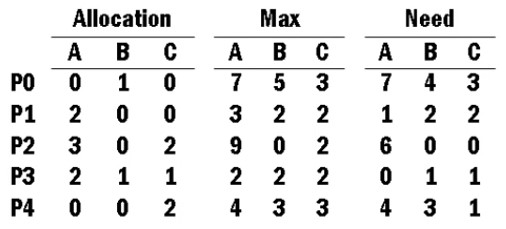
  • 找各 Process 尚需多少資源以完成工作。(即：\(Need[]\))
    • Need = Max – Allocation
  • 求系統目前各類資源的可用數量。(即：\(Available[]\))
    • 題目指出系統提供各類資源的總量分別為：
      • A = 10
      • B = 5
      • C = 7
    • 由上表可知，目前各資源被 Process 所持有之總量分別為：
      • A = 0+2+3+2+0 =7
      • B = 1+0+0+1+0 = 2
      • C = 0+0+2+1+2 = 5
    • 因此，系統目前尚可提供的各類資源總量分別為：
      • A = 10-7 = 3
      • B = 5-2 = 3
      • C = 7-5 = 2
  1. \(P_1\) 提出 \(Request_1[1,0,2]\)，利用 Banker’s Algo. 四個歩驟來分析：
    1. 檢査 \(Request_i\) 是否小於等於 \(Need_i\)，若成立則 go to 2
      • \(P_1\) 的 \(Request = [1, 0, 2]\)，\(Need = [1, 2, 2]\)，∴ 成立
    2. 檢査 \(Request_i\) 是否小於等於 Available ，若成立則 go to 3
      • 系統目前的 \(Available = [3, 3, 2]\)，∴ 成立
    3. (假設性試算) 。
      • \(Available = Available – Request_1 = [3, 3, 2] – [1, 0, 2] = [2, 3, 0]\)
      • \(Need_1\) = \(Need_1\) – \(Request_1 = [1, 2, 2] – [1, 0, 2] = [0, 2, 0]\)
      • \(Allocation_1\) = \(Allocation_1 + Request_1 = [2, 0, 0] + [1, 0, 2] = [3, 0, 2]\)
    4. 執行 Safety Algo.，以判斷系統是否處於 Safe State。若是 Safe 則核准；否則不核准，稍後再來申請。
  • 利用 Safety Algorithm 是否處於 Safe State
    1. 設定初值
      • \(Work = Available = [2, 3, 0]\)
      • 一維布林矩陣 \(Finish[]\) :
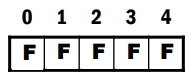
    2. 找到 \(P_1\)，滿足 \(Finish[1] = False\) 且 \(Need_1 ≤ Work\)，then go to 3
    3. 設定 \(Finish[1] = True\)，且 \(Work = Work + Allocation_1 = [5, 3, 2]\)，then go to 2
      • 步驟 2 與 3 執行數次後，可依序找到 \(P_3, P_4, P_0, P_2\) 皆滿足 (此序列不唯一) 。且當執行完 \(P_2\) 後再重執行步驟 2 時，會因不滿足要件而 go to 4
    4. 檢査 Finish Array，皆為 True! ∴ 系統處於 Safe State ⇒ 核准 \(P_1\) 之申請
  • 上述推論找出一組 Safe Sequence: \(P_1, P_3, P_4, P_0, P_2\) (不只一組)
    • 不核准
    • 當執行 Banker’s Algo. 的步驟 2 時，會發現 “檢査 \(Request_4 ≤ Available\)” 不成立，需令 \(P_4\) 等待其它 Process 之資源釋放
    • 不核准
    • 當執行到 Safety Algo. 時，會發現步驟 4 “檢査 Finish 陣列”並不皆為 True，∴ 系統處於 Unsafe ⇒ 否決 \(P_0\) 的申請

Banker’s Algo. 的優缺點

  • 優點： 避免系統發生死結的狀況
  • 缺點： 此 Algo. 需要 \(O(m×n^2)\) 的時間複雜度 (m: 資源種類數; n: Process 個數)，比較耗時。

Dead Lock Avoidance 的重要定理

假設系統包含 m 個單一種類的 Resources，且被 n 個 Process 共用。如果下列兩個條件滿足，則系統無死結存在 (Dead Lock Free)。

  1. \(1≤Max_i≤m\)
  2. \(\sum_{i=1}^nMax_i < m + n\)
  • 問題:
    • 有 6 部印表機提供給 n 個 process 使用，每個 process 之最大需求量為 2。在系統不發生 Dead Lock 的情況下，最多允許多少個 process 在系統內執行? (求 n 的最大値)
  • Ans:
    • 已知 m = 6，\(Max_i\) = 2
    • 條件 1 滿足 (∵ \(1 ≤ Max_i = 2 ≤ 6\))
    • 欲滿足條件 2 (即： \(\sum_{i=1}^nMax_i < m + n\))，則可得 2n < 6 + n → n < 6，∴ n 的最大值為 5。