Tree
Tree 是由 1 個以上的 Nodes 所組成的有限集合,滿足:
- 至少有一個 Node,稱為 Root (
Tree 不可為空) - 其餘的 Nodes 分成 T1, T2, …, Tn 個互斥集合,稱為 Subtree (子集合(子樹)間沒有交集)
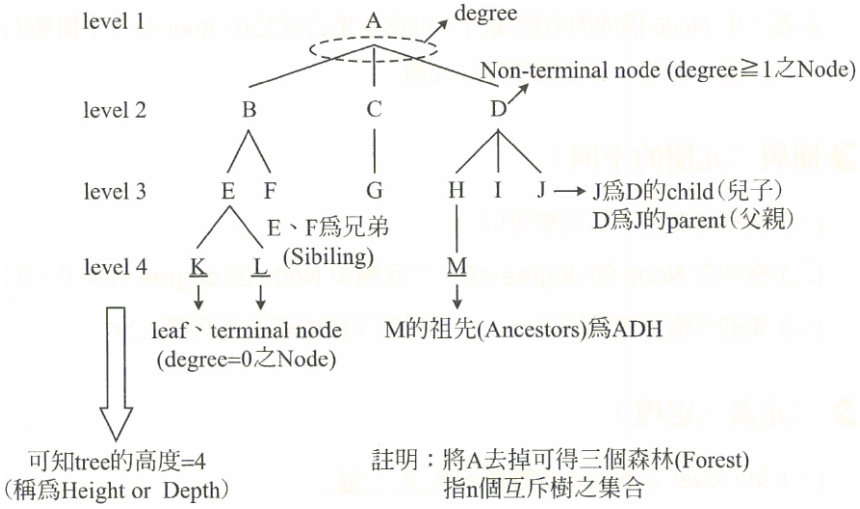
Degree of a node (節點分支度)
節點的子樹個數- Degree of A = 3
- Degree of B = 2
- Degree of E = 0
- Degree of F = 3
- Degrees of C, D, G, H, I are all 0
Degree of a tree (樹分支度)
樹中所有節點分支度最大者。即:Max {各 Node 之 degree}
Leaf (葉子)
分枝度為 0 之節點
Non-leaf Node (Non-terminal Node 或 Internal Node)
樹中所有非葉子的 Node,或是 Degree ≥ 1 的節點稱之
Parent Node (父節點) and Child Node (子節點)
- 若一個節點 x 有後繼節點 (Successor Nodes) ,則此節點 x 即為父節點 (Parent);反之,若一個節點 y 有前輩節點 (Predecessor),則此節點 y 即為子節點 (Child)
- 某節點所有子樹的樹根皆為該節點的 Child; 而該節點為這些樹根的 Parent
Sibling (兄弟)
同一個父節點的所有子節點互稱為 Sibling
Ancestor (袓先)
- 某一個節點的祖先,乃是從樹根到該節點路徑中,所經過的所有節點
- 通常為一
集合 - Ancestors of C: {A, B}

Level (階度)
- 某一個節點的階度,是指
自樹根至該節點的距離 - Root 所在的 level 値為
1,若父點的 level 値為i,則子點的 level 値為i+1 - 下圖:
- E 的 level = 4
- C 的 level = 3
Height (高度;或稱 Depth)
- 一顆樹的各 level 値當中之
最大値,即為該樹的高度 - 上圖:
- 此樹的高度 = 4
Forest (森林)
- 森林及是
n 個互斥樹所形成的集合 (n ≥ 0) - 可以為空
Tree Representation (樹的表示方式)
一顆樹要實作於電腦系統中,通常會採用指標 (Pointer) 來設計
做法1: 直接用 Link list 表示
- 假設 Tree 有 n 個 node,degree 為 k
- Node structure 設計如下:

- 其中
- k: 表示 Tree degree
- Data: 存 node 的資料値
- Link i: 指標指向 ith 子樹之 Root Node (1 ≤ i ≤ k)
- 例如:
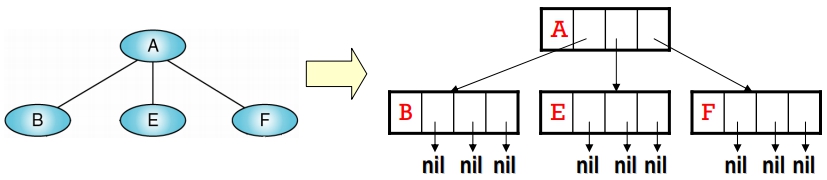
問題:- Link 空間浪費甚巨 (∵空 Link 數目太多)
- 分析:
- 假設 tree 有 n 個 nodes,tree degree 為 k
- 總共的 link 空間為: n
k - 有用的 link 數目為:
n - 1(即 link ≠ nil) - 浪費數目(即: 空 link):
nk - (n-1) - 浪費比例:
做法2: 將 Tree 化成 Binary Tree 後再存
∴ Tree 化成 Binary Tree 是資料結構中的一個很重要的議題