M-way Search Tree

前言： 外部搜尋 (External Search)

m-way Search Tree 主要用於外部搜尋 (External Search)

• 先前的樹状搜尋方法皆為內部搜尋 (Internal Search)( B.S.T.和 AVL )
• Internal Search:
  • 資料量少 ，可以一次全部置於 Memory 中進行 search 之工作
• External Search:
  • 資料量大 ，無法一次全置於 Memory 中，須藉助輔助儲存體( E.g. Disk )，進行分段 search 之工作

• Tree Degree = m，且 m > 2
  • 為何不用二元樹的結構?
    • 因為外部搜尋的資料量頗大，若還是以二元樹的結構存放資料，則樹的高度將很高，資料搜尋將頗為費時
• 目的： 提升 External Search 的效益
  • 要提升 External Search 的效益，則需降低 Disk I/O 的次數
  • 要有效降低 Disk I/O 的次數，則需要降低 Search Tree 的高度
  • 要能夠降低 Search Tree 的高度，則需增大 Tree Degree: m

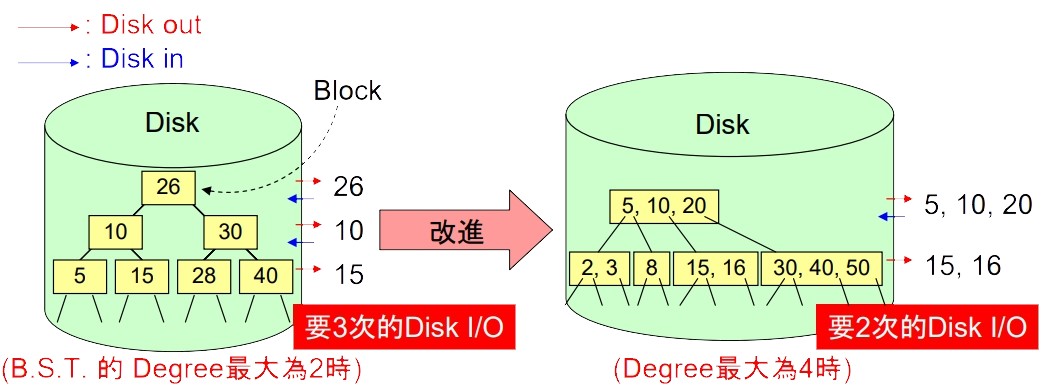
若 m 為無窮大時，雖然高度只有一層，但因為 Data 量太大，無法一次放到 Memory 中。∴ m 以 Memory Size 為限

• 若所有資料可以一次全放到記憶體中，則為 Internal Search 的議題，不需用到外部搜尋的技術

定義

m-way Search Tree T 是一個所有節點的分支度 ≤m 的樹。T 可以是空樹。若 T 不為空樹時，則具有下列性質：

• 節點結構為：
  • 鍵値個數 n ≤ m-1
  • : 鍵値 (資料)
  • : 指標, 指向存放大小介於 與 之間的資料之節點所在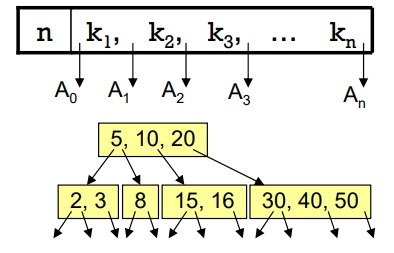
• 節點中的鍵値 (資料) 是由小至大排序的
• 子樹同樣是 m-way Search Tree (遞迴定義)
• 子樹 內的資料均小於鍵値 ；子樹 內的資料均大於鍵値

定理

高度為 h 的 m-way Search Tree：

• 最多的 Node 個數 = ?
• 最多的 Key (Data) 個數 = ? 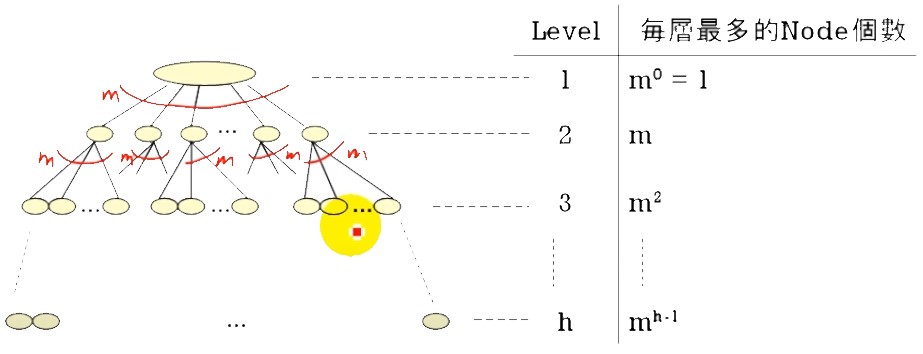∴ 高度為 h 的 m-way Search Tree 最多的 Node 個數 = \[ m^0 + m^1 + m^2 + ... + m^{h-1} = \frac{m^h-1}{m-1} \] ∴ 高度為 h 的 m-way Search Tree 最多的 Data 個數 = \[ \frac{(m - 1) \times (m^h-1)}{m-1} = m^h - 1 \]

思考

m-way Search Tree 雖利用增大 Tree 的 Degree 來降低 Search Tree 的高度，以減少 Disk I/O 的次數，但若此 Tree 不平衡，也可能會變相地增加 Disk I/O 的次數

• 因此發展出 B-tree of order m

參考資料

國立聯合大學陳士杰資料結構