B-Tree
前言
m-way Search Tree 雖利用增大 Tree 的 Degree 來降低 Search Tree 的高度,以減少 Disk I/O 的次數,但若此 Tree 不平衡,也可能會變相地增加 Disk I/O 的次數
- 因此發展出
B-treeof order m
定義
是一個 Balanced m-way search tree。可以為空,若不為空,則滿足:
- Root 至少有 2 個 Childs (
Root: 2 ≤ degree ≤ m) - 除了 Root 及 Failure Node 之外,其餘 Node 的分支度介於 ⎡m/2⎤ 及 m 之間 (
⎡m/2⎤ ≤ degree ≤ m) - 所有的 Failure Node 皆位於同一 Level。(即:所有葉子節點位於同一 Level)
範例
有一 B-tree of order m 如下: 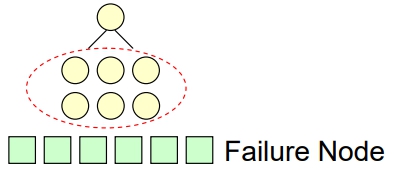
- 若 m = 3 (即:B-tree of order 3)
- Root:2 ≤ degree ≤ 3
- 非 Root 與非外部的節點: ⎡m/2⎤ ≤ degree ≤ m ⇒ 2 ≤ degree ≤ 3
- B-tree of order 3 又稱
2-3 tree
- 若 m = 4 (即:B-tree of order 4)
- Root:2 ≤ degree ≤ 4
- 非 Root 與非外部的節點: ⎡m/2⎤ ≤ degree ≤ m ⇒ 2 ≤ degree ≤ 4
- B-tree of order 4 又稱
2-3-4 tree
- 若 m = 5 (即:B-tree of order 5)
- Root:2 ≤ degree ≤ 5
- 非 Root 與非外部的節點: ⎡m/2⎤ ≤ degree ≤ m ⇒ 3 ≤ degree ≤ 5
定理
高度為 h 的 B-Tree:
- 最多的 Node 個數 = ?
- 最多的 Key (Data) 個數 = ?
由於 B-Tree 中,毎一個節點的 Degree 最大皆可到 m ( m 可自定 )所以其結果等同於 m-way Search Tree 的分析結果
Insert
Step:
- 先做 Search,以找到適當的插入節點,將 x 放入該節點中
- 檢査該節點有無
Overflow無Overflow ( key 數 ≤ m-1 ),則 OK 並跳出有Overflow (key 數 ≥ m)則:- 作 “
Split” 處理 - 針對父點,goto 2 ( 即:作完 Split 後,針對父點檢査是否有 Overflow )
- 作 “
Split
- 將第 ⎡m/2⎤ 個鍵値上拉到父點,其餘鍵値分成左、右兩個子點

範例
- 有一 B-tree of order 3 如下,若連續 Insert “2”, “130”, “8” 會得到什麼結果?
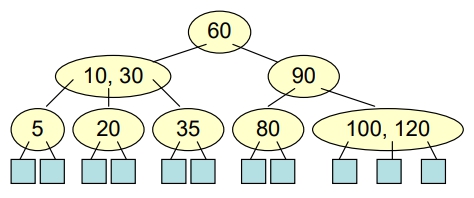
Ans:
- Insert “2”
- 無 Overflow,∴ OK.

- 無 Overflow,∴ OK.
- Insert “130”
- 有 Overflow

- 有 Overflow
- Insert “8”
- 有 Overflow
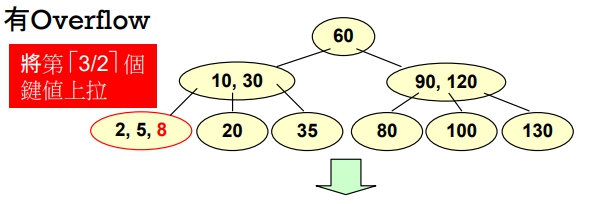

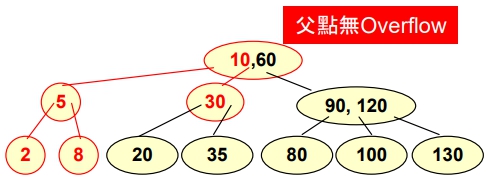
- 有 Overflow
- 給予 1, 2, 3, 4, 5, 6, 7, 8,請建立 2-3 tree (B-tree of order 3)
Ans: 
Delete
Step:
- 先做 Search,以找到 x 所在之節點
- 分成下列兩個 Case 來處理:
Case 1: x 位於 Leaf NodeCase 2: x 位於 Non-leaf Node
Case 1: x 位於 Leaf Node
Step:
- Delete x
- 檢査該 Node 有無
Underflow沒有Underflow (即:鍵値數目 ≥ ⎡m/2⎤ -1) 則 OK,結束工作有Underflow (即:鍵値數目 < ⎡m/2⎤ -1),則:- 先嘗試作 “
Rotation”,若完成工作則結束 - 若無法做 “Rotation”,則作 “
Combination”。Combination 做完,針對父點,goto 2
- 先嘗試作 “
B-tree of order m 中,除了樹根與失敗節點之外,其它的 Internal Node 的 degree 是介於 ⎡m/2⎤ ~ m 之間,∴ 毎個 Internal Node 內的鍵值最多有 m- 1 個鍵値,最少有 ⎡m/2⎤ - 1 個鍵値
Rotation
Rotation 的處理,可分成:
- 右旋:
- 將
右兄弟的最小鍵値傳至父點 - 將原
父點的最大鍵値傳給 Underflow 的節點做為其最大鍵値
- 將
- 左旋:
- 將
左兄弟的最大鍵値傳至父點 - 將原
父點的最小鍵値傳給 Underflow 的節點做為其最小鍵値
- 將
- 這些 Rotation 的結果可保有 Binary Search Tree 的鍵値順序,即:左子樹(小) - 樹根(中) - 右子樹(大)

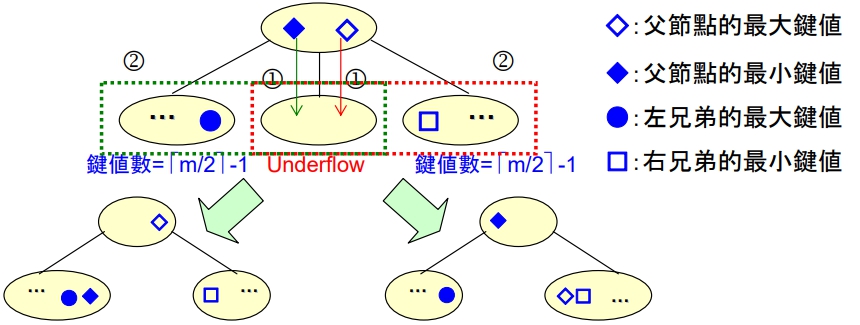
Combination
Combination 的處理,可分成:
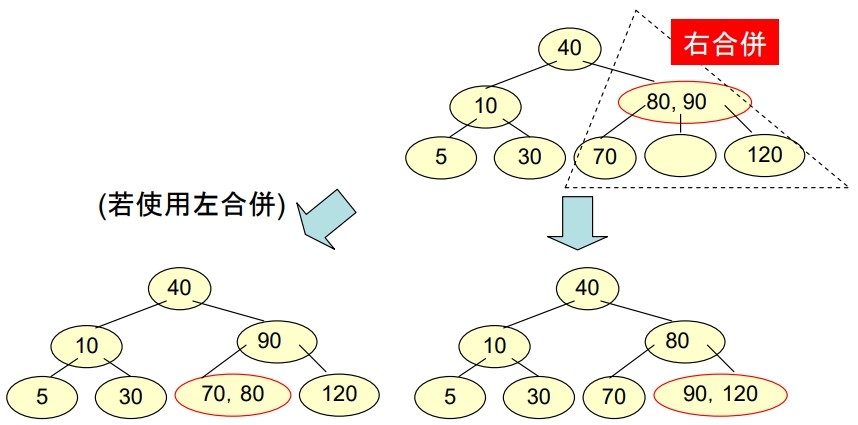
- 右合併:
- 將
父點右邊的最大鍵値傳給 Underflow 的節點做為其最大鍵値 - 將 Underflow 的節點與其
有相同鍵値來源之兄弟合併成一個節點
- 將
- 左合併:
- 將
父點左邊的最小鍵値傳給 Underflow 的節點做為其最小鍵値 - 將 Underflow 的節點與其
有相同鍵値來源之兄弟合併成一個節點
- 將
- 這些 Combination 的結果可保有 Binary Search Tree 的鍵値順序,即:左子樹(小) - 樹根(中) - 右子樹(大)
範例
- 有一 B-tree of order 3 如下,若連續 Delete “5”, “65”, “50” 會得到什麼結果?
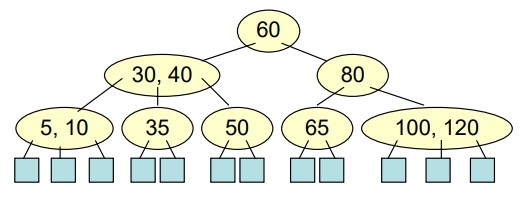
Ans:
2 ≤ degree ≤ 3 ⇒
1 ≤ 鍵値數量 ≤ 2- Delete “5”
- 無 Underflow,∴ OK
- 無 Underflow,∴ OK
- Delete “65”
- 有 Underflow

- 有 Underflow
- Delete “50”
- 有 Underflow
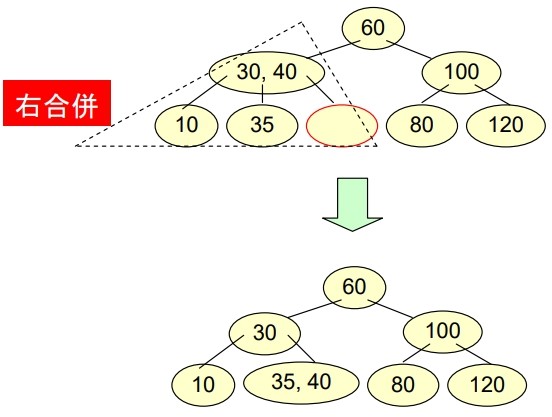
- 有 Underflow
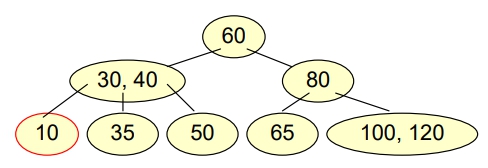
- 有一 B-tree of order 3 如下,若連續 Delete “80”, “10” 會得到什麼結果?
 Ans:
Ans:
2 ≤ degree ≤ 3 ⇒
1 ≤ 鍵値數量 ≤ 2- Delete “80”
- 有 Underflow
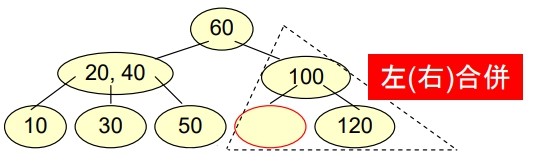
- 有 Underflow
- 父點有 Underflow

- Delete “10”
- 有 Underflow
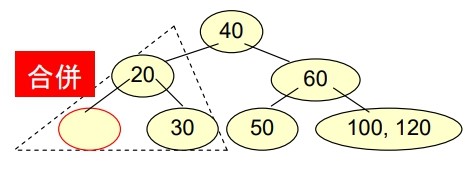
- 有 Underflow
- 父點有 Underflow

父點又有 Underflow

Case 2: x 位於 Non-leaf Node
Step:
- 以
x 的右子樹中之最小鍵値取代 x ;或是 - 以
x 的左子樹中之最大鍵値取代 x
- 以
- 返回 Case 1 作後續處理
範例
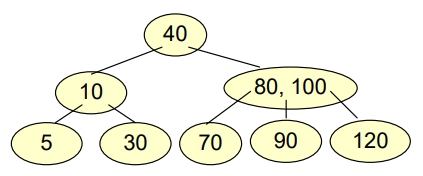
有一 B-tree of order 3 如下,若連續 Delete “60”, “100” 會得到什麼結果? 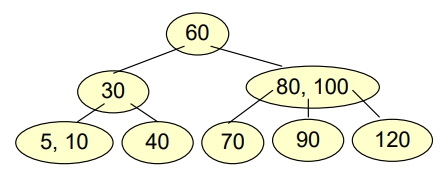
Ans:
2 ≤ degree ≤ 3 ⇒
1 ≤ 鍵値數量 ≤ 2- Delete “60”
- 要選擇
右子樹最小or左子樹最大的鍵値來取代被刪除的資料,以最方便的為優先 - Rotation > Combination
- 要選擇
- 返回 Case 1 做後續處理

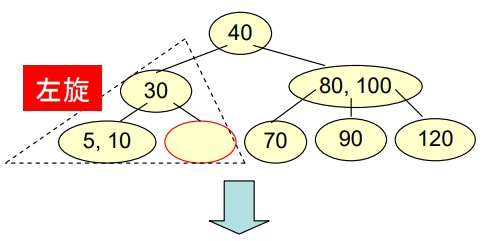
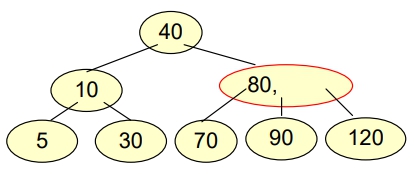
- Delete “100”
- 要選擇右子樹最小 or 左子樹最大的鍵値來取代被刪除的資料,以最方便的為優先
- Rotation > Combination
返回 Case 1 做後續處理
B+ Tree
定義
是 B Tree 之變形,也是用於 External Search / Sort 上- 可以支援 ISAM (Index Sequential Access Method)之實施,常用於 DBMS 內層製作
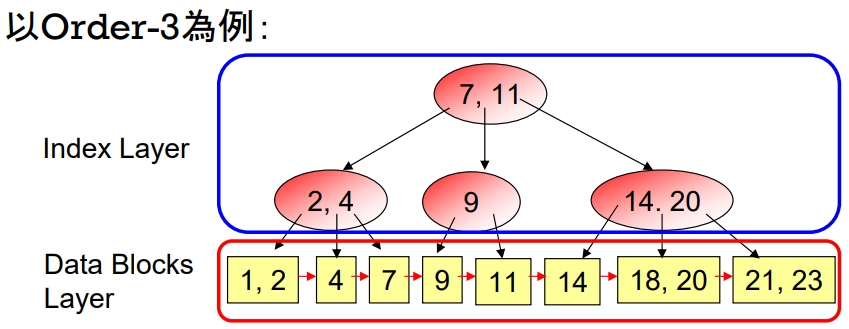
Layer
Index Layer:- 採 B tree 結構。僅用來存放
索引,以幫助 User 正確地找到所需之 Data Block
- 採 B tree 結構。僅用來存放
Data Blocks Layer:- 用以存放
Data,且 Blocks 之間以Link List串連 - Data Block 存放資料時,通常
不會受到 B tree 的 Order 限制。因此,每個 Data Block 最多要塞多少筆 Data 可自訂。當然也可以和 Index Layer 內的節點一致
- 用以存放
Index Sequential Access
- 透過 Index 找到對應的起始 Data Block 之後,即可循序讀取其它資料
- Ex: 找出
大於等於 7 ~ 小於 20的資料